题目内容
【题目】如图,已知在Rt△ABC中,∠ACB=90°,M是边AB的中点,连接CM并延长到点E,使得EM=![]() AB,D是边AC上一点,且AD=BC,联结DE,求∠CDE的度数.
AB,D是边AC上一点,且AD=BC,联结DE,求∠CDE的度数.

【答案】∠CDE=135°.
【解析】
连接AE,先证△AME≌△BMC得AE=BC、∠EAM=∠B,再结合AD=BC、∠BAC+∠B=90°可得AD=AE、∠DAE=90°,据此得出∠ADE=45°,从而得出答案.
如图,连接AE,
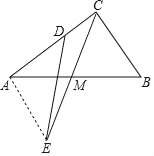
∵∠ACB=90°,AM=BM,
∴CM=![]() AB,
AB,
∵EM=![]() AB,
AB,
∴CM=EM,
在△AME和△BMC中,
∵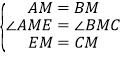 ,
,
∴△AME≌△BMC(SAS),
∴AE=BC,∠EAM=∠B,
∵AD=BC,
∴AD=AE,
∵∠BAC+∠B=90°,
∴∠BAC+∠EAM=90°,即∠DAE=90°,
∴∠ADE=45°,
∴∠CDE=135°.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目



