Question

【题目】如图，四边形为平行四边形，为的中点，连接并延长交 的延长线于点．

（1）求证：△≌△；

（2）过点作于点，为的中点．判断与的位置关系，并说明理由．

Answer 1

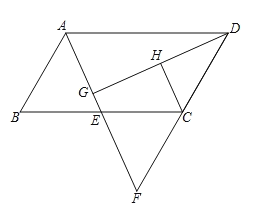
【答案】（1）见解析；（2）CH⊥DG，见解析

【解析】

（1）由平行四边形的性质可得：AB‖DC，则可求出∠BAE=∠CFE，结合题目条件可证得结论；

（2）由（1）可证得CF=CD，可得CH为三角形DFG的中位线，则可得CH‖AF，可证CH⊥DG．

（1）证明：∵四边形ABCD为平行四边形，

∴AB‖DC，

∴∠BAE=∠CFE，

∵E为BC的中点，

∴BE=CE，

在△ABE和△FCE中：

,

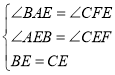∴△ABE△FCE（AAS）；

（2）解：CH⊥DG，

理由如下：由（1）得△ABE△FCE，

∴AB=CF，

∵四边形ABCD为平行四边形，

∴AB=CD，

∴CF=CD，

∴C为FD的中点，

∵为的中点，

∴CH为△DFG的中位线，

∴CH‖AF，

∵DG⊥AE，

∴∠DHC=∠DGF=90°，

∴DG⊥AE．