��Ŀ����
����Ŀ��ij��ѧ��ί��֯���Ļ�����������ɽ��ѧУ�ƻ����˸����轱���ȥ����![]() ���ֽ�Ʒ��
���ֽ�Ʒ��![]() ��������
��������![]() �ͽ�Ʒ������
�ͽ�Ʒ������![]() �ͽ�Ʒ������
�ͽ�Ʒ������![]() ����
����![]() ����
����![]() �ͽ�Ʒ�������ò�����
�ͽ�Ʒ�������ò�����![]() �ͽ�Ʒ�������õ�
�ͽ�Ʒ�������õ�![]() �������ֽ�Ʒ�ĵ������ұ���ʾ������ƻ�
�������ֽ�Ʒ�ĵ������ұ���ʾ������ƻ�![]() �ͽ�Ʒ��
�ͽ�Ʒ��![]() ������
������![]() ����Ʒ���ܷ�����
����Ʒ���ܷ�����![]() Ԫ��
Ԫ��
|
|
| |
����(Ԫ) |
|
|
|
��1������![]() ��
��![]() ֮��ĺ�����ϵʽ��������Ա���
֮��ĺ�����ϵʽ��������Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���������һ�ַ�����ʹ�ù��������ֽ�Ʒ�������ܷ������٣���������ٷ��ã�
���𰸡���1��![]() ��
��![]() ������2������
������2������![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() �������ٷ���Ϊ
�������ٷ���Ϊ![]() Ԫ
Ԫ
��������
(1)�����������B�ͽ�Ʒ��2x-10������C�ͽ�Ʒ��60-3x�������г���ʽw=12x+10��2x-10��+5��60-3x�����ɣ��������ʽ��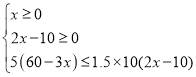 �Ľ⼯���ٸ���A�ͽ�Ʒ��B�ͽ�Ʒ�ĺ�ҪС������50����������𰸣�
�Ľ⼯���ٸ���A�ͽ�Ʒ��B�ͽ�Ʒ�ĺ�ҪС������50����������𰸣�
(2) ����һ�κ������������xȡ��Сʱw��ֵ���ɣ�
![]() �������
�������![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����
![]() ��
��
��������õ�����ʽ�飺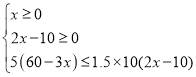
���x��10��
��A�ͽ�Ʒ��B�ͽ�Ʒ�ĺ�ҪС��50����
��x+2x-10��50��
��x��20��
���Ա���x��ȡֵ��Χ��10��x��20��
��w��x֮��ĺ�����ϵʽ��w=17x+200���Ա���x��ȡֵ��Χ��10��x��20��
![]() ��
��![]() ��
�У�
![]()
![]() ��
��![]() �ļ�С����С
�ļ�С����С
![]() ��
��![]() ʱ��
ʱ��![]() ȡ����Сֵ����СֵΪ
ȡ����Сֵ����СֵΪ![]()
��������![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����
��ʹ���������ֽ�Ʒ�������ܷ������٣����ٷ���Ϊ![]() Ԫ��
Ԫ��
�𣺹���A�ͽ�Ʒ10����B�ͽ�Ʒ10����C�ͽ�Ʒ30������ʹ���������ֽ�Ʒ�������ܷ������٣����ٷ���Ϊ370Ԫ��

 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д� �������ϵ�д�
�������ϵ�д�