题目内容
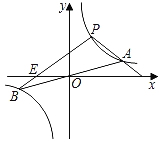
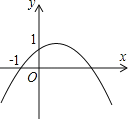
【题目】如图,二次函数![]() (a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②
(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②![]() >4a,③0<b<1,④当x>﹣1时,y>0,其中正确结论的个数是( )
>4a,③0<b<1,④当x>﹣1时,y>0,其中正确结论的个数是( )
A.4个B.3个C.2个D.1个
【答案】B
【解析】
由抛物线的对称轴在y轴右侧,可以判定a、b异号,由此确定①正确;
由抛物线与x轴有两个交点得到b2﹣4ac>0,以及由(0.1)可得:c=1,由此判定②正确;
由抛物线过点(﹣1,0),得出a﹣b+c=0,即a=b﹣1,由a<0得出b<1;由a<0,及ab<0,得出b>0,由此判定③正确;
由图象可知,当x<﹣1时,函数值y<0,由此判定④错误.
解:∵二次函数y=ax2+bx+c(a≠0)过点(0,1)和(﹣1,0),
∴c=1,a﹣b+c=0.
①∵抛物线的对称轴在y轴右侧,
∴x=﹣![]() >0,
>0,
∴a与b异号,
∴ab<0,正确;
②∵抛物线与x轴有两个不同的交点,
∴b2﹣4ac>0,
∴b2>4ac,
由(0.1)可得:c=1
∴b2>4a,正确;
③∵抛物线开口向下,
∴a<0,
∵ab<0,∴b>0.
∵a﹣b+c=0,c=1,
∴a=b﹣1,
∵a<0,
∴b﹣1<0,b<1,
∴0<b<1,正确;
④由图可知,当x<﹣1时,y<0,错误;
综上所述,正确的结论有①②③.
故选:B.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】某超市销售一种高档蔬菜“莼菜”,其进价为16元/kg.经市场调查发现:该商品的日销售量y(kg)是售价x(元/kg)的一次函数,其售价、日销售量对应值如表:
售价 | 20 | 30 | 40 |
日销售量 | 80 | 60 | 40 |
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围);
的函数解析式(不要求写出自变量的取值范围);
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)由于产量日渐减少,该商品进价提高了![]() 元/
元/![]() ,物价部门规定该商品售价不得超过36元/
,物价部门规定该商品售价不得超过36元/![]() ,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求
,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求![]() 的值.
的值.