题目内容
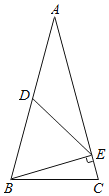
【题目】如图,已知:在△ABC中,∠C=∠ABC,BE⊥AC,△BDE是正三角形.求∠C的度数.
【答案】75°.
【解析】本题首先由等边三角形的性质及垂直定义得到∠DBE=60°,∠BEC=90°,再根据等腰三角形的性质可以得出∠EBC=∠ABC-60°=∠C-60°,最后根据三角形内角和定理得出关系式∠C-60°+∠C=90°解出即可.
解:∵△BDE是正三角形,
∴∠DBE=60°;
∵在△ABC中,∠C=∠ABC,BE⊥AC,
∴∠C=∠ABC=∠ABE+∠EBC则∠EBC=∠ABC﹣60°=∠C﹣60°,∠BEC=90°;
∴∠EBC+∠C=90°,即∠C﹣60°+∠C=90°
解得∠C=75°.
“点睛”本题主要考查等腰三角形的性质及等边三角形的性质及垂直定义,解题的关键是根据三角形内角和定理列出符合题意的简易方程,从而求出结果.

练习册系列答案
相关题目




