Question

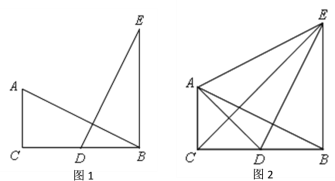
【题目】如图，已知△ABC中，AB＝AC＝6cm，∠B＝∠C，BC＝4cm，点D为AB的中点．

（1）如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

（2）若点Q以1.5cm/s的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，则经过_____秒后，点P与点Q第一次在△ABC的AC边上相遇？（在横线上直接写出答案，不必书写解题过程）

Answer 1

【答案】（1）1cm/s或cm/s；（2）24.

【解析】

（1）由于∠B=∠C，若要△BPD与△CQP全等，只需要BP=CQ或BP=CP，进而求出点Q的速度．

（2）因为点Q的速度大于点P速度，只能是点Q追上点P，即点Q比点P多走AB+AC的路程，据此列出方程，解这个方程即可求得．

（1）设运动时间为t，点Q的速度为v，

∵点D为AB的中点，

∴BD＝3，

∴BP＝t，CP＝4﹣t，CQ＝vt，

由于△BPD≌△CQP，且∠B＝∠C

当BP＝CQ时，

∴t＝vt，

∴v＝1，

当BP＝CP时，

t＝4﹣t，

∴t＝2，

∴BD＝CQ

∴3＝2v，

∴v＝，

综上所述，点Q的速度为1cm/s或cm/s

（2）设经过x秒后P与Q第一次相遇，

依题意得：1.5x＝x+2×6，

解得：x＝24（秒）

此时P运动了24×1＝24（cm）

又∵△ABC的周长为16cm，24＝16+8，

∴点P、Q在AC边上相遇，即经过了24秒，点P与点Q第一次在AC边上相遇．

故答案为24