题目内容
【题目】己知:如图,抛物线![]() 与坐标轴分别交于点
与坐标轴分别交于点![]() , 点
, 点![]() 是线段
是线段![]() 上方抛物线上的一个动点,
上方抛物线上的一个动点,
(1)求抛物线解析式:
(2)当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积最大?
的面积最大?
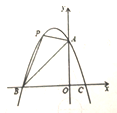
【答案】(1)![]() ;(2)点
;(2)点![]() 运动到坐标为
运动到坐标为![]() ,
,![]() 面积最大.
面积最大.
【解析】
(1)用待定系数法即可求抛物线解析式.
(2)设点P横坐标为t,过点P作PF∥y轴交AB于点F,求直线AB解析式,即能用t表示点F坐标,进而表示PF的长.把△PAB分成△PAF与△PBF求面积和,即得到△PAB面积与t的函数关系,配方即得到t为何值时,△PAB面积最大,进而求得此时点P坐标.
解: (1) ![]() 抛物线
抛物线![]() 过点
过点![]() ,
,
![]() ,
,
解这个方程组,得![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() .
.
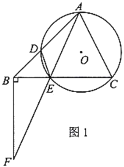
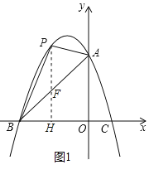
(2)如图1,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() .
.
![]() 时,
时,![]() ,
,
![]() .
.
![]() 直线
直线![]() 解析式为
解析式为![]() .
.
![]() 点
点![]() 在线段
在线段![]() 上方抛物线上,
上方抛物线上,
![]() 设
设![]() .
.
![]() .
.
![]() .
.
![]()
=![]()
![]()
![]()
![]()
![]() 点
点![]() 运动到坐标为
运动到坐标为![]() ,
,![]() 面积最大.
面积最大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目