Question

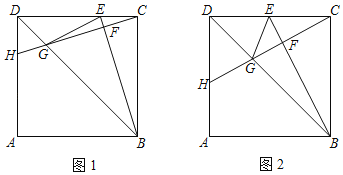
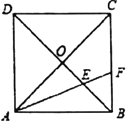
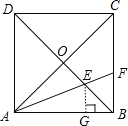
【题目】如图，正方形的对角线、相交于点，的平分线交于点，交于点．若，则____．

Answer 1

【答案】4

【解析】

作EG⊥AB，得△EBG是等腰直角三角形，再利用角平分线的性质可得△EGB是等腰直角三角形，即可求出BE的长，进而可求出OB、BC的长，根据直角三角形两锐角互余的关系可得∠EFB=∠FEB，即可证明BE=BF，根据CF=BC-BF即可得答案.

作EG⊥AB于G，

∵AF是∠CAB的角平分线，OE⊥AC，

∴EG=OE=2，

∵ABCD是正方形，BD是对角线，

∴∠ABE=45°

∴△EBG是等腰直角三角形，

可得BE=EG=2，

∴OB=2+2

∴BC=2OB=4+2

∵∠AFB=90°-∠FAB，∠FEB=∠OEA=90°-∠FAC，∠FAC=∠FAB，

∴∠AFB=∠FEB

∴BF=BE=2

∴CF=BC-BF=4+2-2=4.

故答案为：4