题目内容
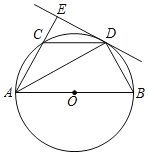
【题目】如图,AB是⊙O的直径,C点在⊙O上,AD平分角∠BAC交⊙O于D,过D作直线AC的垂线,交AC的延长线于E,连接BD,CD.
(1)求证:BD=CD;
(2)求证:直线DE是⊙O的切线;
(3)若DE=![]() ,AB=4,求AD的长.
,AB=4,求AD的长.
【答案】(1)证明见解析;(2)证明见解析;(3)AD=2![]() .
.
【解析】
(1)由角平分线定义得出∠CAD=∠BAD,即可得出结论;
(2)连接半径OD,则OD=OA,得出∠OAD=∠ODA,由∠EAD+∠ADE=90°,∠EAD=∠BAD,得出∠BAD+∠ADE=90°,即∠ODA+∠ADE=90°,即可得出结论;
(3)过点D作DF⊥AB于F,则DF=DE=![]() ,由勾股定理得出OF=
,由勾股定理得出OF=![]() =1,易证△OBD是等边三角形,得出OF=FB=1,AF=AB-FB=3,由勾股定理即可得出结果.
=1,易证△OBD是等边三角形,得出OF=FB=1,AF=AB-FB=3,由勾股定理即可得出结果.
(1)证明:∵在⊙O中,AD平分角∠BAC,
∴∠CAD=∠BAD,
∴BD=CD;
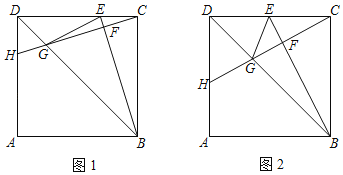
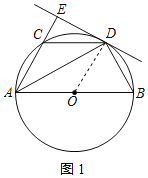
(2)证明:连接半径OD,如图1所示:
则OD=OA,
∴∠OAD=∠ODA,
∵DE⊥AC于E,在Rt△ADE中,
∴∠EAD+∠ADE=90°,
由(1)知∠EAD=∠BAD,
∴∠BAD+∠ADE=90°,即∠ODA+∠ADE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
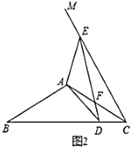
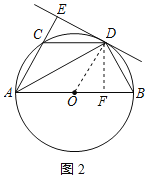
(3)解:过点D作DF⊥AB于F,如图2所示:
则DF=DE=![]() ,
,
∵AB=4,
∴半径OD=2,
在Rt△ODF中,OF=![]() =
=![]() =1,
=1,
∴∠ODF=30°,
∴∠DOB=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴OF=FB=1,
∴AF=AB﹣FB=4﹣1=3,
在Rt△ADF中,AD=![]() =
=![]() =2
=2![]() .
.

练习册系列答案
相关题目