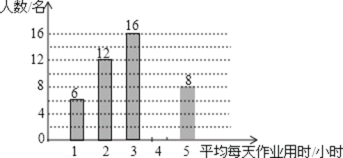
��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC���������㶼�ڸ���ϣ���A������Ϊ��2��4���������������⣺
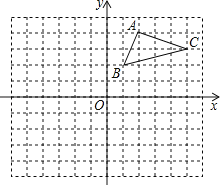
��1��������ABC����x��ԳƵ���A1B1C1����д����C1�����꣨�� ���� ����
��2������ABC����������ĺᡢ�����궼���ԩ�1���ֱ�õ���Ӧ��A2��B2��C2���뻭����A2B2C2����˵����A1B1C1����A2B2C2�Ƿ�����Գ�ͼ�Σ�����ǣ���ô���ǵĶԳ�����ʲô��������ǣ���˵�����ɣ�
���𰸡���1����ͼ��ʾ����A1B1C1��Ϊ���������� 5����3����2����ͼ��ʾ����A2B2C2��Ϊ������������A1B1C1����A2B2C2����Գ�ͼ�Σ��Գ�����y�ᣮ
��������
��1���ֱ���A��B��C����x��ĶԳƵ�A1��B1��C1������A1B1��B1C1��A1C1�����ɻ�����A1B1C1��Ȼ���������ϵ����д����C1�����ꣻ
��2������A��B��C��������꣬�ֱ����A2��B2��C2��A1��B1��C1�����꣬�ٸ�����A1B1C1����A2B2C2�ĸ���������Ĺ�ϵ���ɵó����ۣ�
��1���ֱ���A��B��C����x��ĶԳƵ�A1��B1��C1������A1B1��B1C1��A1C1����ͼ��ʾ����A1B1C1��Ϊ����������ϵ��֪����C1������Ϊ����5��-3����

�ʴ�Ϊ��5��-3��
��2��������ϵ��֪����A��2��4����B��1,2����C��5,3��
��A2��-2��-4����B2��-1,-2����C2��-5,-3����A1��2��-4����B1��1,-2����C1��5,-3��
������ϵ����㣬����A2B2��B2C2��A2C2����ͼ��ʾ����A2B2C2��Ϊ����
����A1B1C1����A2B2C2�ĸ���������ĺ����껥Ϊ�෴�������������
����A1B1C1����A2B2C2����Գ�ͼ�Σ��Գ�����y�ᣮ

 ��У����ϵ�д�
��У����ϵ�д�