题目内容
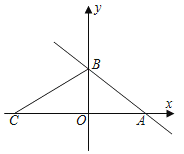
【题目】如图,一次函数y=﹣![]() x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为__.
x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为__.
【答案】(﹣6,0)或(![]() ,0).
,0).
【解析】
根据一次函数求出点A、B的坐标,根据勾股定理即可求出AB,然后根据点A落在y轴的位置分类讨论:当点A落在y轴的正半轴上时,设点C的坐标为(m,0),根据折叠的性质求出A′O和A′C,根据勾股定理列方程即可求出m;当点A落在y轴的负半轴上时,原理同上.
解:∵一次函数y=﹣![]() x+3的图象与x轴交于点A,与y轴交于点B,
x+3的图象与x轴交于点A,与y轴交于点B,
∴A(4,0),B(0,3),
∴OA=4,OB=3,
根据勾股定理可得AB=![]() =5,
=5,
如图1,当点A落在y轴的正半轴上时,

设点C的坐标为(m,0),
∵将△ABC沿BC所在的直线折叠,当点A落在y轴上时,
∴A′O=3+5=8,A′C=AC=4﹣m,
∵A′C2=OC2+A′O2,
∴(4﹣m)2=m2+82,
∴m=﹣6;
如图2,当点A落在y轴的负半轴上时,

设点C的坐标为(m,0),
∵将△ABC沿BC所在的直线折叠,当点A落在y轴上时,
∴A′O=5﹣3=2,A′C=AC=4﹣m,
∵A′C2=OC2+A′O2,
∴(4﹣m)2=m2+22,
∴m=![]() ;
;
综上所述,当点A落在y轴上时,点C的坐标为(﹣6,0)或(![]() ,0),
,0),
故答案为:(﹣6,0)或(![]() ,0).
,0).

【题目】某校组织“大手拉小手,义卖献爱心”活动,计划购买黑白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花4800元购买了 黑白两种颜色的文化衫200件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑 色 文化衫 | 25 | 45 |
白 色 文 化 衫 | 20 | 35 |
(1)学校购进黑.白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.