��Ŀ����
����Ŀ��������������Ƶ�����г��Ϸ������ֳ���������ijҽҩ��˾ÿ�¹̶������ס��������ͺŵķ��������ֹ�20��ֻ�������в�Ʒ����ȫ���۳���ԭ�ϳɱ������۵��ۼ�����������������
| �� | �� |
ԭ�ϳɱ� | 12 | 8 |
���۵��� | 18 | 12 |
������� | 1 | 0.8 |
��1�����ù�˾���·ݵ���������Ϊ300��Ԫ����ס��������ͺŵIJ�Ʒ�ֱ��Ƕ�����ֻ��
��2����˾ʵ�мƼ������ƣ�������ÿ����һֻ���ֻ��һ��������ɣ������˾���·�Ͷ���ܳɱ���ԭ���ܳɱ�+��������ܶ���������239��Ԫ��Ӧ�������żס��������ͺŵIJ�������ʹ���¹�˾���������������������������=�������멁Ͷ���ܳɱ���
���𰸡���1���ס��������ͺŵIJ�Ʒ�ֱ�Ϊ10��ֻ��10��ֻ����2�����ż��ͺŲ�Ʒ����15��ֻ�����ͺŲ�Ʒ����5��ֻʱ���ɻ���������Ϊ91��Ԫ.
��������
�����������1������ͺŵIJ�Ʒ��x��ֻ�������ͺŵIJ�Ʒ����20��x����ֻ��������������Ϊ300��Ԫ���з���18x+12��20��x��=300���ⷽ�̼��ɣ���2���谲�ż��ͺŲ�Ʒ����y��ֻ�������ͺŲ�Ʒ������20��y����ֻ�����ݹ�˾���·�Ͷ���ܳɱ���ԭ���ܳɱ�+��������ܶ���������239��Ԫ�г�����ʽ���������ʽ�Ľ⼯ȷ����y�ķ�Χ���ٸ�������=�ۼ����ɱ��г�W��y��һ�κ���������y�ķ�Χȷ����W�����ֵ���ɣ�
�����������1������ͺŵIJ�Ʒ��x��ֻ�������ͺŵIJ�Ʒ����20��x����ֻ��
��������ã�18x+12��20��x��=300��
��ã�x=10��
��20��x=20��10=10��
��ס��������ͺŵIJ�Ʒ�ֱ�Ϊ10��ֻ��10��ֻ��
��2���谲�ż��ͺŲ�Ʒ����y��ֻ�������ͺŲ�Ʒ������20��y����ֻ��
��������ã�13y+8.8��20��y����239��
��ã�y��15��
������������W=��18��12��1��y+��12��8��0.8����20��y��=1.8y+64��
��y=15ʱ��W������ֵΪ91��Ԫ��
�����ż��ͺŲ�Ʒ����15��ֻ�����ͺŲ�Ʒ����5��ֻʱ���ɻ���������Ϊ91��Ԫ.

 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�����Ŀ��������������Ƶ�����г��Ϸ������ֳ���������ijҽҩ��˾ÿ�¹̶������ס��������ͺŵķ��������ֹ�20��ֻ�������в�Ʒ����ȫ���۳���ԭ�ϳɱ������۵��ۼ�����������������
| �� | �� |
ԭ�ϳɱ� | 12 | 8 |
���۵��� | 18 | 12 |
������� | 1 | 0.8 |
��1�����ù�˾���·ݵ���������Ϊ300��Ԫ����ס��������ͺŵIJ�Ʒ�ֱ��Ƕ�����ֻ��
��2����˾ʵ�мƼ������ƣ�������ÿ����һֻ���ֻ��һ��������ɣ������˾���·�Ͷ���ܳɱ���ԭ���ܳɱ�+��������ܶ���������239��Ԫ��Ӧ�������żס��������ͺŵIJ�������ʹ���¹�˾���������������������������=�������멁Ͷ���ܳɱ���
����Ŀ��ijʳƷ��˾����һ��ʳƷ����֪ÿ�µ������ɱ�y1�����x֮����һ�κ�����ϵ������y1���Ա���z��kg���IJ��ֶ�Ӧֵ���±���
x�����kg�� | 10 | 20 | 30 |
y1����λ��/Ԫ�� | 3030 | 3060 | 3090 |
��1����y1��x֮��ĺ�����ϵʽ��
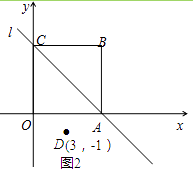
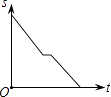
��2�������������֣�����ʳƷÿ�µ���������y2��Ԫ��������x��kg��֮��������ͼ��ʾ�ĺ�����ϵ 
��y2��x֮��ĺ�����ϵʽΪ��
��3���ڼ���ù�˾ÿ�������ĸ���ʳƷ����ȫ���۳�����ô�ù�˾ÿ������Ҫ��������ʳƷ����kg���Ų������