题目内容
【题目】已知四边形OABC是边长为4的正方形,分别以OA,OC所在的直线为x轴、y轴,建立如图1所示的平面直角坐标系,直线l经过A,C两点.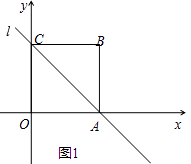
(1)写出点A,点C坐标并求直线l的函数表达式;
(2)若P是直线l上的一点,当△OPA的面积是5时,请求出点P的坐标;
(3)如图2,点D(3,﹣1),E是直线l上的一个动点,求出使|BE﹣DE|取得最大值时点E的坐标和最大值(不需要证明).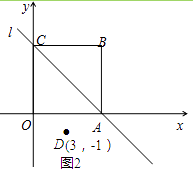
【答案】
(1)
解:∵四边形OABC是边长为4的正方形,
∴A(4,0)和C(0,4);
设直线l的函数表达式y=kx+b(k≠0),经过A(4,0)和C(0,4)
得 ![]() ,
,
解之得 ![]() ,
,
∴直线l的函数表达式y=﹣x+4
(2)
解:设△OPA底边OA上的高为h,由题意等 ![]() ×4×h=5,
×4×h=5,
∴h= ![]() ,
,
∴|﹣x+4|= ![]() ,解得x=
,解得x= ![]() 或
或 ![]()
∴P1( ![]() ,
, ![]() )、P2(
)、P2( ![]() ,
, ![]() )
)
(3)
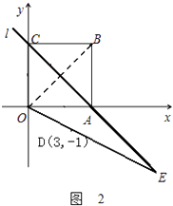
解:∵O与B关于直线l对称,
∴连接OD并延长交直线l于点E,则点E为所求,此时|BE﹣DE|=|OE﹣DE|=OD,OD即为最大值,如图2.
设OD所在直线为y=k1x (k1≠0),经过点D(3,﹣1),
∴﹣1=3k1,
∴k1= ![]()
∴直线OD为 ![]() ,
,
解方程组: 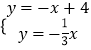 ,得
,得 ![]() ,
,
∴点E的坐标为(6,﹣2).
又D点的坐标为(3,﹣1)
由勾股地理可得OD= ![]() .
.
【解析】(1)易得A,C两点的坐标,设出一次函数解析式,把这两点代入可得所求函数解析式;(2)设△OPA底边OA上的高为h,根据绝对值的定义分两种情况解答即可;(3)连接OD并延长交直线l于点E,得到DB的解析式与l的解析式联立可得E的坐标.
【考点精析】通过灵活运用一次函数的图象和性质,掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
| 甲 | 乙 |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入﹣投入总成本)