题目内容
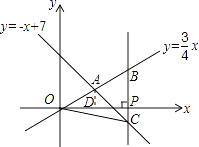
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y= ![]() x与一次函数y=﹣x+7的图象交于点A.
x与一次函数y=﹣x+7的图象交于点A. 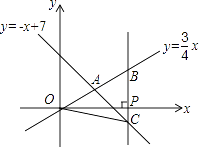
(1)求点A的坐标;
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y= ![]() x和y=﹣x+7的图象于点B,C,连接OC.若BC=
x和y=﹣x+7的图象于点B,C,连接OC.若BC= ![]() OA,求△OBC的面积.
OA,求△OBC的面积.
【答案】
(1)解:∵由题意得, 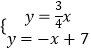 ,解得
,解得 ![]() ,
,
∴A(4,3)
(2)解:过点A作x轴的垂线,垂足为D,在Rt△OAD中,由勾股定理得,
OA= ![]() =
= ![]() =5.
=5.
∴BC= ![]() OA=
OA= ![]() ×5=7.
×5=7.
∵P(a,0),
∴B(a, ![]() a),C(a,﹣a+7),
a),C(a,﹣a+7),
∴BC= ![]() a﹣(﹣a+7)=
a﹣(﹣a+7)= ![]() a﹣7,
a﹣7,
∴ ![]() a﹣7=7,解得a=8,
a﹣7=7,解得a=8,
∴S△OBC= ![]() BCOP=
BCOP= ![]() ×7×8=28.
×7×8=28.
【解析】(1)联立两一次函数的解析式求出x、y的值即可得出A点坐标;(2)过点A作x轴的垂线,垂足为D,在Rt△OAD中根据勾股定理求出OA的长,故可得出BC的长,根据P(a,0)可用a表示出B、C的坐标,故可得出a的值,由三角形的面积公式即可得出结论.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
【题目】由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
| 甲 | 乙 |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入﹣投入总成本)