题目内容
【题目】如图,已知抛物线 ![]() 与x轴交于点A,B,与y轴负半轴交于点C且OB=OC,点P为抛物线上的一个动点,且点P位于x轴下方,点P与点C不重合。
与x轴交于点A,B,与y轴负半轴交于点C且OB=OC,点P为抛物线上的一个动点,且点P位于x轴下方,点P与点C不重合。
(1)求抛物线的解析式
(2)若△PAC的面积为 ![]() ,求点P的坐标
,求点P的坐标
(3)若以A、B、C、P为顶点的四边形面积记作S,则S取何值时,对应的点P有且只有2个?
【答案】
(1)解:∵抛物线y= ![]() x2+ax+4a与y轴负半轴交于点C,
x2+ax+4a与y轴负半轴交于点C,
∴C(0,4a),4a<0,
∵OB=OC,
∴B(-4a,0),
∵B在抛物线上,
∴ ![]() (-4a)2+a(-4a)+4a=0,
(-4a)2+a(-4a)+4a=0,
解得a=0或a=-1,
∵a<0,
∴a=-1,
∴抛物线的解析式为y= ![]() x2-x-4;
x2-x-4;
(2)解:设P(m, ![]() m2-m-4),
m2-m-4),
由y= ![]() x2-x-4得A(-2,0),B(4,0),C(0,-4),
x2-x-4得A(-2,0),B(4,0),C(0,-4),
①如图1,P在B、C之间时,即0<m<4,设PA与y轴交于D,
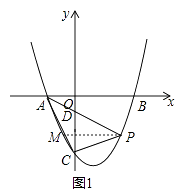
∵A(-2,0),P(m, ![]() m2-m-4),
m2-m-4),
∴直线PA的解析式为y= ![]() (m-4)(x+2),
(m-4)(x+2),
∴D(0,m-4),
∴CD=m,
∴S△PAC= ![]() DC(xP-xA)=
DC(xP-xA)= ![]() m(m+2),
m(m+2),
∵△PAC的面积为 ![]() ,
,
∴ ![]() m(m+2)=
m(m+2)= ![]() ,
,
解得m=-1± ![]() ,
,
∵0<m<4,
∴m=-1+ ![]() ,
,
yP=- ![]() -2
-2 ![]() ,故P(-1+
,故P(-1+ ![]() ,-
,- ![]() -2
-2 ![]() );
);
②如图2,点P在A、C之间时,即-2<m<0,过P作y轴平行线交于AC于D点,
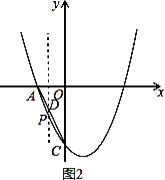
∵A(-2,0),C(0,4),
∴直线AC的解析式为y=-2x-4,
∴D(m,-2m-4),
∴PD=-2m-4-( ![]() m2-m-4)=-
m2-m-4)=- ![]() m2-m,
m2-m,
∴S△PAC= ![]() PD(xC-xA)=-
PD(xC-xA)=- ![]() m2-m,
m2-m,
∴- ![]() m2-m=
m2-m= ![]() ,解得m=-1,
,解得m=-1,
∴P(-1,- ![]() ),
),
综上,符合条件的点P有两个,分别是(-1+ ![]() ,-
,- ![]() -2
-2 ![]() )或(-1,-
)或(-1,- ![]() );
);
(3)解;由题意可得:P(m, ![]() m2-m-4),
m2-m-4),
①如图3,当点P在A、C之间时,即-2<m<0,连接AC,
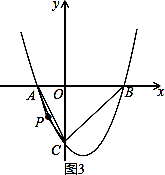
则S四边形APCB=S△PAC+S△ABC,
由(2)得S△PAC=- ![]() m2-m,
m2-m,
∵A(-2,0),B(4,0),C(0,-4),
∴S△ABC= ![]() ABCO=1,
ABCO=1,
∴S=- ![]() m2-m+12=-
m2-m+12=- ![]() (m+1)2+
(m+1)2+ ![]() ,
,
∵-2<m<0,
∴12≤S≤ ![]() ,
,
此时当12≤S≤ ![]() 时,对应的点P有且只有2个;当S=
时,对应的点P有且只有2个;当S= ![]() 时,对应的点P有且只有1个.
时,对应的点P有且只有1个.
②如图4,当点在B、C之间时,即0<m<4,连接PA,
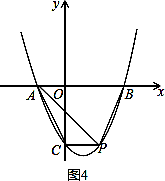
则S四边形APCB=S△PAC+S△APB,
由(2)得S△PAC= ![]() m(m+2),
m(m+2),
又S△PAB= ![]() AB×|yP|,
AB×|yP|,
∵P在第四象限,
∴yP<0,
∴S△PAB= ![]() ×AB×|yP|=
×AB×|yP|= ![]() ×6×(-
×6×(- ![]() m2+m+4),
m2+m+4),
∴S=S△ACP+S△APB=-m2+4m+12=-(m-2)2+16,
∵0<m<4,12<S≤ ![]() ,
,
此时当12<S<16时,对应的点P有且只有2个,
当S=16时,对应的点P有且只有1个,
由①②得:
当12≤S≤ ![]() ,对应的点P有且只有2个;
,对应的点P有且只有2个;
当S= ![]() 时,对应的点P有且只有1个;
时,对应的点P有且只有1个;
当12<S<16时,对应的点P有且只有2个,
当S=16时,对应的点P有且只有1个;
综上所述: ![]() <S<16时,对应的点P有且只有2个.
<S<16时,对应的点P有且只有2个.
【解析】(1)可利用二次函数图像的特殊点加上所给条件,易得a=-1,解得二次函数解析式
(2)由于p在x轴下方,考虑实际情况,可能出现y轴左右两种情况,所以要分情况讨论,在利用坐标轴把三角形分为两个以坐标轴为底边的三角形,结合所给数据,还有△PAC的面积为 ![]() 可列方程从而得到m的值,再得到点p的坐标,需要注意的是保证所取得的坐标在取值范围之内。
可列方程从而得到m的值,再得到点p的坐标,需要注意的是保证所取得的坐标在取值范围之内。
(3)由(2)可知要分情况讨论,利用(2)所得的数据可以计算出每一段函数中p对应的个数,从而取得点P有且只有2个时S的取值范围

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】两枚正四面体骰子的各面上分别标有数字1,2,3,4,现在同时投掷这两枚骰子,并分别记录着地的面所得的点数为a、b.
(1)假设两枚正四面体都是质地均匀,各面着地的可能性相同,请你在下面表格内列举出所有情形(例如(1,2),表示a=1,b=2),并求出两次着地的面点数相同的概率.
b | 1 | 2 | 3 | 4 |
1 | (1,2) | |||
2 | ||||
3 | ||||
4 |
(2)为了验证试验用的正四面体质地是否均匀,小明和他的同学取一枚正四面体进行投掷试验.试验中标号为1的面着地的数据如下:
试验总次数 | 50 | 100 | 150 | 200 | 250 | 600 |
“标号1”的面着地的次数 | 15 | 26 | 34 | 48 | 63 | 125 |
“标号1”的面着地的频率 | 0.3 | 0.26 | 0.23 | 0.24 |
请完成表格(数字精确到0.01),并根据表格中的数据估计“标号1的面着地”的概率是多少?


