题目内容
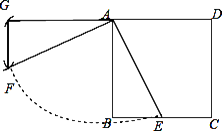
【题目】如图,正方形ABCD的边长为2,E是BC的中点,以点A为中心,把△ABE绕点A顺时针旋转90°,设点E的对应点为F.
(1)画出旋转后的三角形.(尺规作图,保留作图痕迹,不写作法)
(2)求点E运动到点F所经过的路径的长
【答案】
(1)解:如图,△AGF为所作;
(2)解:∵E是BC的中点,
∴BE=1,AB=2
∴AE= ![]() ,
,
∵△ABE绕点A顺时针旋转90°得到△AGF,
∴∠EAF=90°,
∴点E运动到点F所经过的路径的长= ![]() =
= ![]()
【解析】(1)做旋转图像三步:连接特殊点与对称中心;以对称中心为顶点,特殊点与对称中心连线为起始边,沿旋转方向做角;在另一边截取特殊点与对称中心连线段的长度。
(2)旋转后点所走过的路径是一段弧,所以找到半径AE和圆心角∠EAF易得弧长,即点E运动到点F所经过的路径的长
【考点精析】解答此题的关键在于理解图形的旋转的相关知识,掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

【题目】近期,大陆相关部门对原产台湾地区的15种水果实施进口零关税措施,扩大了台湾水果在大陆的销售,某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:
每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
每天销量(千克) | 50 | 52 | 54 | 56 | … | 86 |
设当单价从38元/千克下调了x元时,销售量为y千克.
(1)写出y与x之间的关系式;
(2)如果凤梨的进价是20元/千克,某天的销售价定为30元/千克,这天的销售利润是多少?
(3)以前在两岸未直接通航时,运输要绕行,需耗时一周(七天),凤梨最长的保存期为一个月(30天),若每天售价不低于30元/千克,一次进货最多只能是多少千克?




