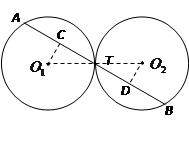
题目内容
已知⊙ 、⊙
、⊙ 外切于点
外切于点 ,经过点
,经过点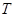 的任一直线分别与⊙
的任一直线分别与⊙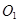 、⊙
、⊙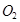 交于点
交于点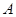 、
、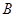 ,
,
(1)若⊙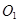 、⊙
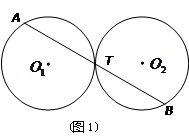
、⊙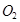 是等圆(如图1),求证
是等圆(如图1),求证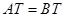 ;
;
(2)若⊙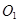 、⊙
、⊙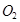 的半径分别为
的半径分别为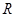 、
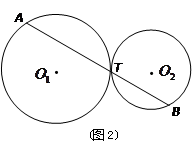
、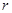 (如图2),试写出线段
(如图2),试写出线段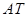 、
、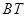 与
与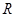 、
、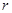 之间始终存在的数量关系(不需要证明).
之间始终存在的数量关系(不需要证明).
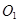 、⊙
、⊙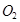 外切于点
外切于点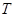 ,经过点
,经过点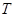 的任一直线分别与⊙
的任一直线分别与⊙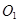 、⊙
、⊙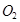 交于点
交于点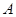 、
、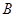 ,
,(1)若⊙
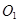 、⊙
、⊙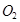 是等圆(如图1),求证
是等圆(如图1),求证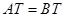 ;
;(2)若⊙
 、⊙
、⊙ 的半径分别为
的半径分别为 、
、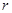 (如图2),试写出线段
(如图2),试写出线段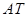 、
、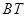 与
与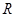 、
、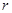 之间始终存在的数量关系(不需要证明).
之间始终存在的数量关系(不需要证明).

解:(1)联结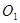
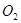 .
.
∵⊙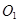 .⊙
.⊙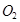 外切于点
外切于点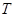 ,∴点T在
,∴点T在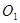
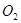 上.
上.
如图,过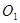 .
.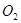 分别作
分别作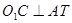 .
.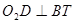 ,垂足为
,垂足为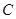 、
、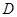 ,
,
∴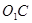 ∥
∥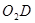 .
.
∴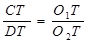 .
.
∵⊙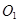 .⊙
.⊙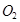 是等圆,∴
是等圆,∴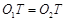 .
.
∴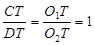 ,
,
∴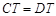 .
.
在⊙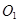 中,
中,
∵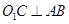 ,
,
∴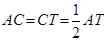 .
.
同理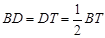 .
.
∴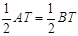 ,即
,即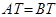 .
.
(2)线段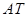 .
.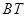 与
与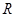 、
、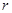 之间始终存在的数量关系是
之间始终存在的数量关系是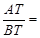
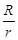 .
.
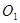
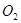 .
.∵⊙
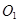 .⊙
.⊙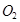 外切于点
外切于点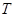 ,∴点T在
,∴点T在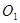
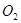 上.
上. 如图,过
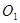 .
.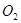 分别作
分别作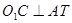 .
.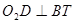 ,垂足为
,垂足为 、
、 ,
, 
∴
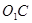 ∥
∥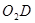 .
. ∴
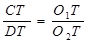 .
. ∵⊙
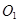 .⊙
.⊙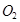 是等圆,∴
是等圆,∴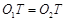 .
. ∴
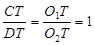 ,
,∴
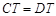 .
. 在⊙
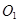 中,
中,∵
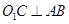 ,
,∴
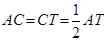 .
. 同理
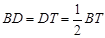 .
. ∴
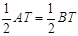 ,即
,即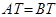 .
. (2)线段
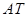 .
.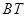 与
与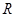 、
、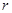 之间始终存在的数量关系是
之间始终存在的数量关系是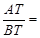
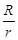 .
. (1)连接O1O2,如图1所示,根据两圆外切时,两圆心连线过切点,得到O1O2过T点,由垂直得到一对直角相等,再由对顶角相等,利用两对对应角相等的两三角形相似得到△O1CT与△O2DT,由相似得比例,又两圆为等圆,半径相等可得出,可得出CT=DT,又O1C⊥AT,利用垂径定理得到CT等于AT的一半,同理DT等于BT的一半,等量代换可得出AT=BT,得证;
(2)线段AT、BT与R、r之间始终存在的数量关系是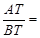
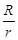 ,理由为:连接O1O2,如图2所示,根据两圆外切时,两圆心连线过切点,得到O1O2过T点,由垂直得到一对直角相等,再由对顶角相等,利用两对对应角相等的两三角形相似得到△O1CT与△O2DT,由相似得比例,将O1T=R,O2T=r代入,得到CT与DT的比值为R:r,又O1C⊥AT,利用垂径定理得到CT等于AT的一半,同理DT等于BT的一半,等量代换可得出AT与BT的比值为R:r.
,理由为:连接O1O2,如图2所示,根据两圆外切时,两圆心连线过切点,得到O1O2过T点,由垂直得到一对直角相等,再由对顶角相等,利用两对对应角相等的两三角形相似得到△O1CT与△O2DT,由相似得比例,将O1T=R,O2T=r代入,得到CT与DT的比值为R:r,又O1C⊥AT,利用垂径定理得到CT等于AT的一半,同理DT等于BT的一半,等量代换可得出AT与BT的比值为R:r.
(2)线段AT、BT与R、r之间始终存在的数量关系是
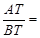
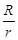 ,理由为:连接O1O2,如图2所示,根据两圆外切时,两圆心连线过切点,得到O1O2过T点,由垂直得到一对直角相等,再由对顶角相等,利用两对对应角相等的两三角形相似得到△O1CT与△O2DT,由相似得比例,将O1T=R,O2T=r代入,得到CT与DT的比值为R:r,又O1C⊥AT,利用垂径定理得到CT等于AT的一半,同理DT等于BT的一半,等量代换可得出AT与BT的比值为R:r.
,理由为:连接O1O2,如图2所示,根据两圆外切时,两圆心连线过切点,得到O1O2过T点,由垂直得到一对直角相等,再由对顶角相等,利用两对对应角相等的两三角形相似得到△O1CT与△O2DT,由相似得比例,将O1T=R,O2T=r代入,得到CT与DT的比值为R:r,又O1C⊥AT,利用垂径定理得到CT等于AT的一半,同理DT等于BT的一半,等量代换可得出AT与BT的比值为R:r.
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 的坐标为
的坐标为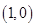 ,点
,点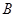 的坐标为
的坐标为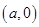 ,圆
,圆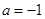 时,点
时,点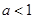 时,点
时,点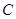 .当
.当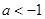 时,点
时,点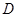 .当
.当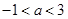 时,点
时,点 为圆心,任意长为半径画弧,与射线
为圆心,任意长为半径画弧,与射线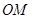 交于点
交于点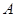 ,再以
,再以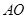 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点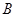 ,画射线
,画射线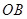 ,则
,则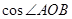 的值等于 .
的值等于 .
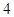 ,其中一个圆的半径长为
,其中一个圆的半径长为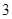 ,那么当两圆内切时,另一圆的半径为 .
,那么当两圆内切时,另一圆的半径为 .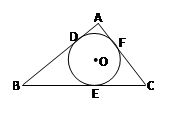
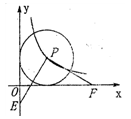
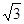 D、10+
D、10+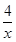 上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是 ___________.
上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是 ___________.