题目内容
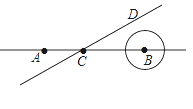
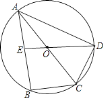
【题目】如图,⊙O是△ABC的外接圆,AC是直径,点E是AB的中点,延长EO交⊙O于D点,若BC=DC,AB=2 ![]() ,求
,求 ![]() 的长度.
的长度.
【答案】![]() .
.
【解析】
连结BD,如图,利用圆心角、弧、弦的关系,由BC=DC得![]() ,则根据垂径定理得到AC垂直平分BD,所以AB=AD,同样可得DA=DB,则可判断△ABD为等边三角形,所以∠BAC=30°,∠ABD=60°,根据圆周角定理得∠AOD=2∠ABD=120°,然后在Rt△AEO中计算出AO,最后利用弧长公式计算即可.
,则根据垂径定理得到AC垂直平分BD,所以AB=AD,同样可得DA=DB,则可判断△ABD为等边三角形,所以∠BAC=30°,∠ABD=60°,根据圆周角定理得∠AOD=2∠ABD=120°,然后在Rt△AEO中计算出AO,最后利用弧长公式计算即可.
连结BD,如图,
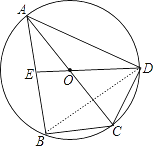
∵BC=DC,
∴![]() ,
,
∴AC垂直平分BD,
∴AB=AD,
∵点E是AB的中点,即AE=BE![]() ,
,
∴DE⊥AB,
∴DA=DB,
∴AB=AD=DB,
∴△ABD为等边三角形,
∴∠BAC=30°,∠ABD=60°,
∴∠AOD=2∠ABD=120°,
在Rt△AEO中,∵∠EAO=30°,
∴OE=![]() AE=1,AO=2OE=2,
AE=1,AO=2OE=2,
∴![]() 的长度=
的长度= ![]() =
=![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目