题目内容
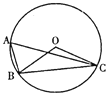
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 、
、![]() 为
为![]() 上两点,
上两点,![]() ,
,![]() ,垂足为
,垂足为![]() .直线
.直线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求证:![]() .
.
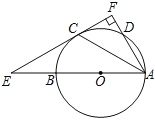
【答案】(1)EF与⊙O相切,理由见解析;(2)证明见解析.
【解析】
(1)连接OC,由题意可得∠OCA=∠FAC=∠OAC,可得OC∥AF,可得OC⊥EF,即EF是⊙O的切线;
(2) 连接BC,根据直径所对圆周角是直角证得△ACF∽△ABC,即可证得结论.
(1)EF与⊙O相切,
理由如下:
如图,连接OC,

∵![]() ,
,
∴∠FAC=∠BAC,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OCA=∠FAC,
∴OC∥AF,
又∵EF⊥AF,
∴OC⊥EF,
∴EF是⊙O的切线;
(2)连接BC,
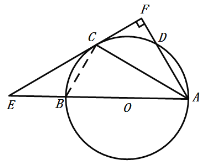
∵AB为直径,
∴∠BCA=90°,
又∵∠FAC=∠BAC,
∴△ACF∽△ABC,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
【题目】商场销售某种冰箱,该种冰箱每台进价为2500元,已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了![]() 元.
元.
(1)填表:
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到最大时,则每台冰箱的实际售价应定为多少元?