题目内容
【题目】每年九月开学前后是文具盒的销售旺季,商场专门设置了文具盒专柜李经理记录了![]() 天的销售数量和销售单价,其中销售单价
天的销售数量和销售单价,其中销售单价![]() (元/个)与时间第
(元/个)与时间第![]() 天(
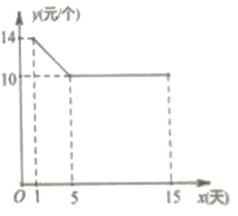
天(![]() 为整数)的数量关系如图所示,日销量
为整数)的数量关系如图所示,日销量![]() (个)与时间第
(个)与时间第![]() 天(
天(![]() 为整数)的函数关系式为:
为整数)的函数关系式为: 
![]() 直接写出
直接写出![]() 与
与![]() 的函数关系式,并注明自变量
的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
![]() 设日销售额为
设日销售额为![]() (元) ,求
(元) ,求![]() (元)关于
(元)关于![]() (天)的函数解析式;在这
(天)的函数解析式;在这![]() 天中,哪一天销售额
天中,哪一天销售额![]() (元)达到最大,最大销售额是多少元;
(元)达到最大,最大销售额是多少元;
![]() 由于需要进货成本和人员工资等各种开支,如果每天的营业额低于
由于需要进货成本和人员工资等各种开支,如果每天的营业额低于![]() 元,文具盒专柜将亏损,直接写出哪几天文具盒专柜处于亏损状态
元,文具盒专柜将亏损,直接写出哪几天文具盒专柜处于亏损状态
【答案】(1)y=![]() ,(2)w=
,(2)w=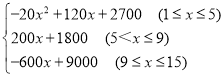 ,在这15天中,第9天销售额达到最大,最大销售额是3600元,(3)第13天、第14天、第15天这3天,专柜处于亏损状态.
,在这15天中,第9天销售额达到最大,最大销售额是3600元,(3)第13天、第14天、第15天这3天,专柜处于亏损状态.
【解析】
(1)用待定系数法可求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)利用总销售额=销售单价×销售量,分三种情况,找到![]() (元)关于
(元)关于![]() (天)的函数解析式,然后根据函数的性质即可找到最大值.
(天)的函数解析式,然后根据函数的性质即可找到最大值.
(3)先根据第(2)问的结论判断出在这三段内哪一段内会出现亏损,然后列出不等式求出x的范围,即可找到答案.
解:(1)当![]() 时,设直线的表达式为
时,设直线的表达式为![]()
将![]() 代入到表达式中得
代入到表达式中得
![]() 解得
解得![]()
∴当![]() 时,直线的表达式为
时,直线的表达式为![]()
∴ y=![]() ,
,
(2)由已知得:w=py.
当1≤x≤5时,w=py=(-x+15)(20x+180)=-20x2+120x+2700
=-20(x-3)2+2880,当x=3时,w取最大值2880,
当5<x≤9时,w=10(20x+180)=200x+1800,
∵x是整数,200>0,
∴当5<x≤9时,w随x的增大而增大,
∴当x=9时,w有最大值为200×9+1800=3600,
当9<x≤15时,w=10(-60x+900)=-600x+9000,
∵-600<0,∴w随x的增大而减小,
又∵x=9时,w=-600×9+9000=3600.
∴当9<x≤15时,W的最大值小于3600
综合得:w=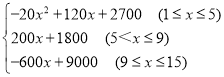 ,
,
在这15天中,第9天销售额达到最大,最大销售额是3600元.
(3)当![]() 时,
时,
当![]() 时,y有最小值,最小值为
时,y有最小值,最小值为![]()
∴不会有亏损
当![]() 时,
时,
当![]() 时,y有最小值,最小值为
时,y有最小值,最小值为![]()
∴不会有亏损
当![]() 时,
时,
![]()
解得![]()
∵x为正整数
∴![]()
∴第13天、第14天、第15天这3天,专柜处于亏损状态.

【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).