题目内容
【题目】如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有________.(填上所有正确结论的序号)

【答案】①②③④
【解析】
连接![]() ,证明
,证明![]() ,利用等腰三角形的性质可判断结论①;由线段垂直平分线的性质定理,等腰三角形的判定与性质,三角形的内角和定理,角的和差求出∠APO与∠DCO的和等于30°,再证明
,利用等腰三角形的性质可判断结论①;由线段垂直平分线的性质定理,等腰三角形的判定与性质,三角形的内角和定理,角的和差求出∠APO与∠DCO的和等于30°,再证明![]() 是等边三角形,可判断结论②,③;, 在线段AC上截取AE=AP,连接PE,证明△APO≌△EPC可判断结论④.
是等边三角形,可判断结论②,③;, 在线段AC上截取AE=AP,连接PE,证明△APO≌△EPC可判断结论④.
解:如图,连接![]()
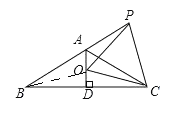
∵AD⊥BC,![]()
![]() 是
是![]() 的中垂线,
的中垂线,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]() 即结论①正确;
即结论①正确;
连接BO,如图1所示:
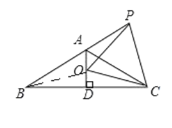
![]()
![]()
由![]()
![]()
![]()
![]()
![]()
![]() 是等边三角形,
是等边三角形,
![]()
![]()
即结论②正确;
![]() 是等边三角形,
是等边三角形,
![]()
即结论③正确;
在线段AC上截取AE=AP,连接PE,如图所示:
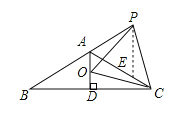
∵∠BAC+∠CAP=180°,∠BAC=120°,
∴∠CAP=60°,
∴△APE是等边三角形,
∴AP=EP,
又∵△OPC是等边三角形,
∴OP=CP,
又∵∠APE=∠APO+∠OPE=60°,
∠CPO=∠CPE+∠OPE=60°,
∴∠APO=∠EPC,
在△APO和△EPC中,
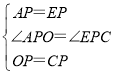 ,
,
∴△APO≌△EPC(SAS),
∴AO=EC,
又∵AC=AE+EC,AE=AP,
∴AC=AO+AP, 即结论④正确;
综合所述,①,②,③,④都正确,
故答案为:①,②,③,④.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目