题目内容
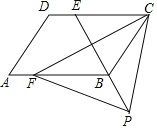
【题目】在等腰△ABC中,AB=AC,将线段BA绕点B顺时针旋转到BD,使BD⊥AC于H,连结AD并延长交BC的延长线于点P.
(1)依题意补全图形;
(2)若∠BAC=2α,求∠BDA的大小(用含α的式子表示);
(3)小明作了点D关于直线BC的对称点点E,从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.

【答案】(1)补图见解析;(2)∠BDA=45°+α;(3)证明见解析.
【解析】试题分析:
(1)按要求在图中画出相应图形即可;
(2)由∠BAC=2α结合BD⊥AC于点H,可得∠ABH=90°-2α,再结合BD=AB即可求得∠BDA;
(3)首先按要求补充完整图形,由点D和点E关于BP对称,可得BE=BD=AC,DE=2DG,DE⊥BP,∠DBP=∠EBP,结合(2)中结论,可证得∠DBE=2α=∠BAC,从而可证得△ABC≌△BDE,由此可得BC=DE;由∠P=∠ADB-∠DBP可得∠P=45°,结合DE⊥BP可得![]() ,结合BC=DE=2DG即可得到DG与DP间的数量关系了.
,结合BC=DE=2DG即可得到DG与DP间的数量关系了.
试题解析:
(1)将图形按要求补充完整如下:

(2)∵BD⊥AC于点H,
∴∠AHB=90°,
又∵∠BAC=2α,
∴∠ABH=90°-2α,
∵BA=BD
∴∠BDA=∠BAD= ![]() ;
;
(3)补全图形,如下图所示:

证明过程如下:
∵D关于BC的对称点为E,且DE交BP于G,
∴DE⊥BP,DG=GE,∠DBP=∠EBP,BD=BE,
∵AB=AC,∠BAC=2α
∴∠ABC=∠ACB= ![]() ,
,
由(2)知∠ABH=90°-2α,
∴∠DBP=90°-α-(90°-2α)=α
∴∠DBP=∠EBP=α
∴∠BDE=2α
∵AB=BD=AC=BE,
∴△ABC≌△BDE,
∴BC=DE,
∵∠DPB=∠ADB-∠DBP=45°+α-α=45°,∠DGP=90°,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴BC=![]() DP.
DP.