题目内容
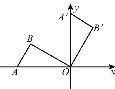
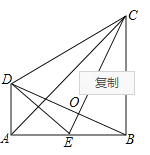
【题目】如图,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 交
交![]() 于点
于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 垂直平分
垂直平分![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的是( )
.其中正确的是( )
A.①②③B.①③⑤C.①②④D.②③④
【答案】A
【解析】
由BC⊥AB,DA⊥AB,CE⊥BD,得到∠ADB=∠EBC=∠COB=90°,根据余角的性质得到∠ABD=∠BCE,证得△ABD≌△BCE,得到①正确;由线段垂直平分线的性质得到②正确;根据等腰三角形的性质等边对等角,得到③正确;因为∠CED+∠EDO=90°,∠DBC+∠OCB=90°,BE≠DE,∠EDB≠∠OCB,∠CED≠∠DBC,得到④不正确;由CE=CD,CE>BC,得到CD>BC,所以⑤不正确.
解:∵BC⊥AB,DA⊥AB,CE⊥BD,
∠ADB=∠EBC=∠COB=90°,
∴∠ABD+∠CBD=∠OCB+∠ABD=90°,
∴∠ABD=∠BCE,
在△ABD与△BCE中,

∴△ABD≌△BCE,
∴AD=BE,
∴①正确;
∵AE=BE,∴AD=AE,
∵∠CAB=∠DAE=45°,
∴AC垂直平分DE,
∴②正确;
∵AC垂直平分DE,
∴CD=CE,
∵CE=BD,
∴CD=BD,
∴∠DBC=∠DCB,
∴③正确;
∵∠CED+∠EDO=90°,∠DBC+∠OCB=90°,
∵BE≠DE,
∴∠EDB≠∠OCB,
∴∠CED≠∠DBC,
∴④不正确;
∵CE=CD,CE>BC,CD>BC,
∴⑤不正确.
故选:A.

 金博士一点全通系列答案
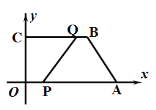
金博士一点全通系列答案【题目】如图,在△ABC中,AE平分∠BAC交BC于点E,D是AB边上一动点,连接CD交AE于点P,连接BP.已知AB =6cm,设B,D两点间的距离为xcm,B,P两点间的距离为y1cm,A,P两点间的距离为y2cm.
小明根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
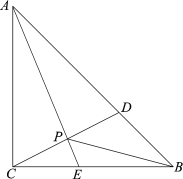
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 0.00 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,![]() ),并画出函数y1,
),并画出函数y1,![]() 的图象;
的图象;

(3)结合函数图象,回答下列问题:
①当AP=2BD时,AP的长度约为 cm;
②当BP平分∠ABC时,BD的长度约为 cm.
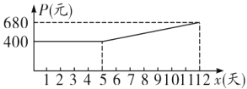
【题目】某制药厂需要紧急生产一批能有效缓解“新冠肺炎”的药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量![]() (吨)是时间
(吨)是时间![]() (天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本
(天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本![]() (元)与时间
(元)与时间![]() (天)的关系满足如图所示的函数图象.
(天)的关系满足如图所示的函数图象.
时间 | 2 | 4 |
每天产量 | 24 | 28 |
(1)求药品每天的产量![]() (吨)与时间
(吨)与时间![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)当![]() 时,直接写出
时,直接写出![]() (元)与时间
(元)与时间![]() (天)的函数关系是
(天)的函数关系是![]() ;
;
(3)若这批药品的价格为1400元/吨,每天的利润设为![]() 元,求哪一天的利润最高,最高利润是多少?(利润
元,求哪一天的利润最高,最高利润是多少?(利润![]() 售价
售价![]() 成本)
成本)