题目内容
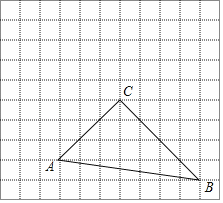
【题目】如图,在每个小正方形的边长为1的网格中,△ABC的顶点A、B、C均在格点上.
(1)∠ACB的大小为 ;
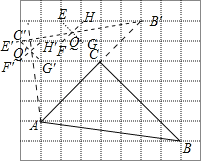
(2)在如图所示的网格中以A为中心,取旋转角等于∠BAC,把△ABC逆时针旋转,请用无刻度的直尺,画出旋转后的△AB'C',保留作图痕迹,不要求证明;
(3)点P是BC边上任意一点,在(2)的旋转过程中,点P的对应点为P',当线段CP'最短时,CP'的长度为 .
【答案】(1)90°;(2)见解析;(3)![]()
【解析】
(1)利用勾股定理的逆定理即可解决问题.
(2)如图,延长AC到格点B′,使得AB′=AB=![]() ,取格点E,F,G,H,连接EG,FH交于点Q,取格点E′,F′.G′,H′,连接E′G′,F′H′交于点Q′,作直线AQ′,直线B′Q交于点C′,△AB′C′即为所求.
,取格点E,F,G,H,连接EG,FH交于点Q,取格点E′,F′.G′,H′,连接E′G′,F′H′交于点Q′,作直线AQ′,直线B′Q交于点C′,△AB′C′即为所求.
(3)通过将点B以A为中心,取旋转角等于∠BAC旋转,找到线段BC旋转后所得直线FG,只需找到点C到FG的垂足即为P′.
(1)由网格图可知
![]() ,
,![]() ,
,![]() ,
,
∵AC2+BC2=AB2
∴由勾股定理逆定理,△ABC为直角三角形.
∴∠ACB=90°
故答案为:90°.
(2)如图,延长AC到格点B′,使得AB′=AB=![]() ,取格点E,F,G,H,连接EG,FH交于点Q,取格点E′,F′.G′,H′,连接E′G′,F′H′交于点Q′,作直线AQ′,直线B′Q交于点C′,△AB′C′即为所求.
,取格点E,F,G,H,连接EG,FH交于点Q,取格点E′,F′.G′,H′,连接E′G′,F′H′交于点Q′,作直线AQ′,直线B′Q交于点C′,△AB′C′即为所求.
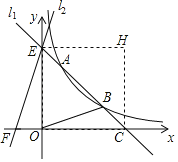
(3)作图过程如下:
取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G:取格点F,连接FG交TC延长线于点P′,则点P′即为所求
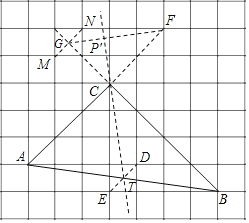
证明:连CF
∵AC,CF为正方形网格对角线
∴A、C、F共线
∴![]() ,
,
由图形可知:![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∵∠GCF=∠ACB,
,∵∠GCF=∠ACB,
∴△ACB∽△GCF
∴∠GFC=∠B
∵![]()
∴当BC边绕点A逆时针旋转∠CAB时,点B与点F重合,点C在射线FG上.
由作图可知T为AB中点
∴∠TCA=∠TAC
∴∠F+∠P′CF=∠B+∠TCA=∠B+∠TAC=90°
∴CP′⊥GF
此时,CP′最短
故答案为:如图,取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G:取格点F,连接FG交TC延长线于点P′,则点P′即为所求.

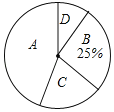
【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调査(问卷调査表如图所示),将调査结果整理后绘制例图1、图2两幅均不完整的统计图表.
最受欢迎的校本课程调查问卷
您好!这是一份关于您最喜欢的校本课程问卷调查表,请在表格中选择一个(只能选一个)您最喜欢的课程选项,在其后空格内打“√”,非常感谢您的合作.
选项 | 校本课程 | |
A | 3D打印 | |
B | 数学史 | |
C | 诗歌欣赏 | |
D | 陶艺制作 |
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B | 0.25 | |
C | 16 | b |
D | 8 | |
合计 | a | 1 |
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调査结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.