题目内容
【题目】如图,△ABC是等腰直角三角形,∠BCA=90°,BC=AC,直角顶点C在y轴上,锐角顶点A在x轴上.
(1)如图①,若点C的坐标是(0,-1),点A的坐标是(-3,0),求B点的坐标;
(2)如图②,若x轴恰好平分∠BAC,BC与x轴交于点D,过点B作BE⊥x轴于E,问AD与BE有怎样的数量关系,并说明理由;
(3)如图③,直角边AC在两坐标轴上滑动,使点B在第四象限内,过B点作BF⊥x轴于F,在滑动的过程中,猜想OC、BF、OA之间的关系,并证明你的结论.
【答案】(1)(1,2);(2)AD=2BE,理由见解析;(3)OC=BF+OA,证明见解析;
【解析】
(1)如图①,过B作BG⊥y轴于G,证明△AOC≌△CGB(AAS),得AO=CG=3,OC=BG=1,表示点B的坐标;
(2)如图②,延长BE、AC交于H,证明△AEB≌△AEH(ASA),得BE=EH,即BH=2BE,再证明△ACD≌△BCH(ASA),可得结论;
(3)如图③,过C作CM⊥BF,交FB的延长线于M,证明△AOC≌△BMC(AAS),四边形OCMF为矩形,根据线段的和可得结论.
(1)如图①,过B作BG⊥y轴于G,
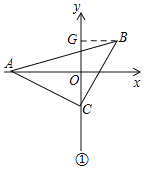
∵点C的坐标是(0,-1),点A的坐标是(-3,0),
∴OC=1,OA=3,
∵∠BCA=90°,
∴∠ACO+∠BCG=90°,
∵∠BCG+∠CBG=90°,
∴∠ACO=∠CBG,
∵AC=BC,∠AOC=∠BGC=90°,
∴△AOC≌△CGB(AAS),
∴AO=CG=3,OC=BG=1,
∴OG=3-1=2,
∴B(1,2);
(2)如图②,AD=2BE,
理由是:延长BE、AC交于H,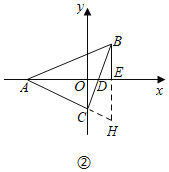
∵BE⊥x轴,
∴∠AEB=∠AEH=90°,
∵AE平分∠BAC,
∴∠CAD=∠BAD,
∵AE=AE,
∴△AEB≌△AEH(ASA),
∴BE=EH,即BH=2BE,
∵∠ACD=∠BED=90°,∠ADC=∠BDE,
∴∠CAD=∠CBH,
∵AC=BC,∠ACD=∠BCH=90°,
∴△ACD≌△BCH(ASA),
∴AD=BH=2BE;
(3)OC=BF+OA,
理由是:如图③,过C作CM⊥BF,交FB的延长线于M,
同理可得:△AOC≌△BMC(AAS),
∴AO=BM,OC=CM,
∵∠COF=∠OFM=∠M=90°,
∴四边形OCMF为矩形,
∴FM=OC,
∴FM=BF+BM,
∴OC=BF+OA.