题目内容
【题目】在下列括号内填理由：已知：如图，AC∥DE，CD、EF分别为∠ACB、∠DEB的平分线．
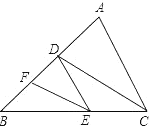
求证：CD∥EF
证明：∵AC∥DE〔已知）
∴ ＝ （ ）
∵CD、EF分别为∠ACB、∠DEB的平分线．（已知）
，
（ ）
∴∠DCB＝∠FEB
∴CD∥EF（ ）
【答案】∠ACB；∠BED；两直线平行，同位角相等；∠ACB；∠BED；角平分线的定义；同位角相等，两直线平行
【解析】
根据平行线的性质和判定，以及角平分线的定义就进行证明即可．
证明：∵AC∥DE（已知）
∴∠ACB＝∠BED（ 两直线平行，同位角相等）
∵CD、EF分别为∠ACB、∠DEB的平分线．（已知）
（角平分线的定义）
∴∠DCB＝∠FEB
∴CD∥EF（ 同位角相等，两直线平行），
故答案为：∠ACB；∠BED；两直线平行，同位角相等；∠ACB；∠BED；角平分线的定义；同位角相等，两直线平行．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
