题目内容
【题目】如图，ABCD中，AE平分∠BAD交BC边于E，EF⊥AE交CD边于F，延长BA到点G，使AG=CF，连接GF，若BC=7，DF=3，AE=
，则GF的长为__________
【答案】3
．
【解析】
首先延长AE、DC相交于点M，过点A作AH⊥BC于点H，连接AC，进而得出FC的长，再利用勾股定理得出EH的长，即可得出FG的长
延长AE、DC相交于点M，过点A作AH⊥BC于点H，连接AC，
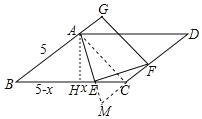
∵AB∥DM，
∴∠M=∠BAE，∠CEM=∠DAM，
而∠BAE=∠DAM，
∴∠M=∠CEM=∠DAM，
∴CE=CM，DM=AD=7，
∵∠M+∠MFE=90°=∠CEM+∠CEF，
∴∠MFE=∠CEF，
∴CF=CE=CM=
FM=（MD-DF）=2，
∴AB=DC=DF+CF=5，BE=BC-CE=5，
设EH=x，可得：BH=5-x，
∵AH2=AE2-EH2=AB2-BE2，
∴10-x2=25-（5-x）2
解得：x=1，
则EH=1，AH=3，
故CH=CE+EH=3，
则AC=
=3，
而四边形ACFG是平行四边形，
故FG=AC=3．
故答案为：3．
期末宝典单元检测分类复习卷系列答案
【题目】如图，设 A 是由n×n 个有理数组成的n 行n 列的数表， 其中aij （ i，j =1，2，3，，n ）表示位于第i 行第 j 列的数，且aij 取值为 1 或－1.
a | a | a | |
a | a | a | |
a | a | a |
对于数表 A 给出如下定义：记 xi 为数表 A 的第i 行各数之积，y j 为数表 A 的第 j 列各数之积.令S = (x1+ x2++ x
)+(y1+ y2+ y)，将S 称为数表 A 的“积和”.
（1）当n = 4 时，对如下数表 A，求该数表的“积和” S 的值；
1 | 1 | －1 | －1 |
1 | －1 | 1 | 1 |
1 | －1 | －1 | 1 |
－1 | －1 | 1 | 1 |
（2）是否存在一个 3×3 的数表 A，使得该数表的“积和” S =0 ？并说明理由；
（3）当n =10 时，直接写出数表 A 的“积和” S 的所有可能的取值.
