题目内容
【题目】已知,在△ABC中,AC=BC,∠ACB=90°,直线CP不过点A,B,且不平分∠ACB,点B关于直线CP的对称点为E,直线AE交直线CP于点F.
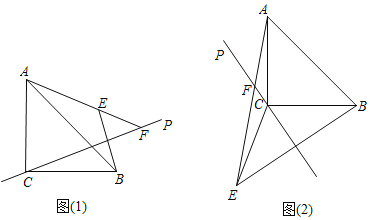
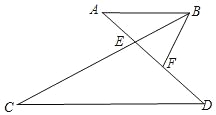
(1)如图1,直线CP与线段AB相交,若∠PCB=25°,求∠CAF的度数;
(2)如图1,当直线CP绕点C旋转时,记∠PCB=α(0°<α<90°,且α≠45°).
①∠FEB的大小是否改变,若不变,求出∠FEB的度数;若改变,请用含α的式子表示).
②找出线段AF,EF,BC的数量关系,并给出证明.
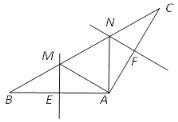
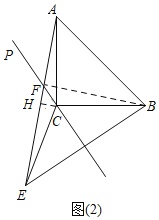
(3)如图2,当直线CP在△ABC外侧,且0°<∠ACP<45°时.若BC=5![]() ,EF=8,求CF的长.
,EF=8,求CF的长.
【答案】(1)∠CAF=70°;(2)①∠FEB的大小不变,都是45°;②AF2+EF2=2BC2,理由见解析;(3)CF=![]()
【解析】
(1)如图1,根据轴对称的性质得:CB=CE,∠ECP=∠PCB=25°,由等边对等角和三角形内角和可得结论;
(2)①存在两种情况:当P在直线BC的上方时,根据CB=CE,CP⊥BE,得∠PCB=∠ECP=α,计算∠AEC=45°+α,∠CEB=90°﹣α,根据角的和可得∠AEB=135°,最后由平角的定义得结论;
当P在直线BC的下方时,同得可得∠FEB的度数是45°;
②连接FB,证明∠AFB=90°,根据勾股定理可得结论;
(3)连接BF,过C作CH⊥AE,同(2)可得:∠EFC=45°,AF2+EF2=2BC2,根据△ACE是等腰三角形和勾股定理可计算CF的长.
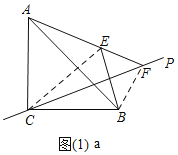
解:(1)如图(1)a,连接CE,
∵B、E关于CP对称,
∴CB=CE,∠ECP=∠PCB=25°,
∵CB=CA,
∴CE=CA,
∵∠ACB=90°,
∴∠ACE=40°,
∴∠CAF=70°;
(2)①如图(1),∠FEB的大小不变,
当PC在CB的上方时,如图(1)a,
∵∠PCB=α,则∠ECP=α,
∴∠ACE=90°﹣2α,∠AEC=45°+α,∠CEB=90°﹣α,
∴∠AEB=135°
∴∠FEB=45°;
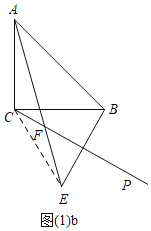
当PC在CB的下方时,如图(1)b,连接CE,
∵∠PCB=∠ECP=α,
∴∠ACE=90°+2α,∠AEC=45°﹣α,∠CEB=90°﹣α,
∴∠AEB=∠FEB=∠CEB﹣∠AEC=(90°﹣α)﹣(45°﹣α)=45°,
综上,∠FEB的大小不变,都是45°;
②AF2+EF2=2BC2,理由是:
连接FB,
∵点B关于直线CP的对称点为E,∠FEB=∠FBE=45°,
∴∠AFB=90°,
∴AF2+FB2=AB2,
∵AB2=2BC2,EF=BF,
∴AF2+EF2=2BC2;
(3)连接BF,过C作CH⊥AE,
同(2):记∠PCB=α,则∠PCE=α
∴∠ACP=α﹣90°
∴∠ACE=2α﹣90°
∵AC=CE
∴∠AEC=![]() =135°﹣α
=135°﹣α
∵∠CEB=α﹣90°
∴∠FEB=α﹣90°+135°﹣α=45°
可得:∠EFC=45°,
∴∠EFC=∠BFC=45°
∴∠AFB=90°
同理得:AF2+EF2=2BC2,
∵BC=5![]() ,EF=8,
,EF=8,
∴AF=6,
∴AE=14,
∵BC=CE=AC,
∴AH=7,
∴FH=1,
∴CF=![]() .
.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案