题目内容
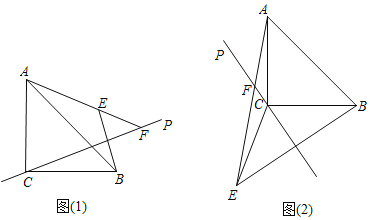
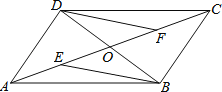
【题目】四边形ABCD为平行四边形,AC为对角线,∠BAC=60°,CE、BF分别∠ACB、∠ABC的角平分线,CE、BF相交于G;
(1)求∠CGF的度数;
(2)求证:BE+CF=BC;
(3)若BE:CF=1:2,EG=2![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.
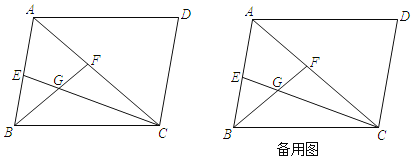
【答案】(1)60°;(2)见解析;(3)180![]()
【解析】
(1)由角平分线的性质和三角形内角和定理可求解;
(2)在BC边上截取CN=CF,连接GN,由“SAS”可证△CGN≌△CG,可得∠CGN=∠CGF=60°,可得∠BGN=∠BGE,由“ASA”可证△BGN≌△BGE,可得BE=BN,可得结论;
(3)设BE=a,CF=2a,AE=c,AF=b,由相似三角形的性质列出方程组,求出 ,通过证明△ABF∽△GEB,可得
,通过证明△ABF∽△GEB,可得![]() ,可求c的值,可得AB,AC,BC的值,即可求平行四边形ABCD的面积.
,可求c的值,可得AB,AC,BC的值,即可求平行四边形ABCD的面积.
解:(1)∵∠BAC=60°,
∴∠ABC+∠ACB=120°,
∵CE、BF分别∠ACB、∠ABC的角平分线,
∴∠GBC+∠GCB=![]() ×120°=60°,
×120°=60°,
∴∠BGC=120°,
∴∠CGF=60°;
故答案为:60°.
(2)在BC边上截取CN=CF,连接GN,如图所示:

在△CGN和△CGF中,
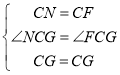 ,
,
∴△CGN≌△CGF(SAS),
∴∠CGN=∠CGF,GF=GN
∵∠BGC=120°,∠CGF=60°,
∴∠BGN=60°,∠EGF=120°,
∴∠BGE=360°﹣120°﹣120°﹣60°=60°,
∴∠BGN=∠BGE,
在△BGN和△BGE中,
 ,
,
∴△BGN≌△BGE(ASA),
∴BE=BN,EG=GN
∴EG=GN=GF
∵BC=BN+CN=BE+CF,
∴BE+CF=BC;
(3)如图,延长CE,DA交于点H,延长BF交AD于点P,过点B作BM⊥AC于M,
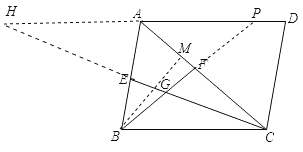
∵BE:CF=1:2,
∴设BE=a,CF=2a,
由(2)可知BC=BE+CF=a+2a=3a,
∵四边形ABCD是平行四边形
∴AD∥BC
∴∠H=∠BCE,∠APB=∠FBC,
∵CE、BF分别∠ACB、∠ABC的角平分线
∴∠ACE=∠BCE,∠ABF=∠CBF
∴∠H=∠ACE,∠APB=∠ABF
∴AH=AC,AP=AB,
设AE=c,AF=b,
∴AB=c+a,AC=b+2a,
∵AH∥BC
∴△AHE∽△BCE
∴![]()
∴![]()
∴b+2a=3c①
∵AH∥BC
∴△APF∽△CBF
∴![]()
∴![]()
∴c+a=![]() b②
b②
由①②组成方程组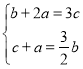
解得:
∴AB=![]() c,AC=3c,
c,AC=3c,
由(2)可知FG=EG=2![]()
∵∠EGB=∠BAC=60°,∠ABF=∠GBE,
∴△ABF∽△GEB,
∴![]()
∴
∴BG=3![]() ,c=8
,c=8
∴a=7,b=10
∴AB=15,AC=24,BC=21,
∵∠BAC=60°,BM⊥AC
∴AM=![]() AB=
AB=![]() ,BM=
,BM=![]() AM=
AM=![]() ,
,
∴SABCD=2S△ABC=2×![]() ×
×![]() ×24=180
×24=180![]()
故答案为:180![]() .
.