Question

【题目】如图，在△ABC中，AB=AC，∠BAC=120°，AB的垂直平分线交AB于E，交BC于M，AC的垂直平分线交AC于F，交BC于N．连接AM、AN．

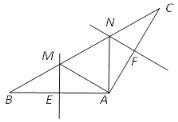
（1）求∠MAN的大小；

（2）求证：BM=CN．

Answer 1

【答案】（1）∠MAN=60°；（2）见解析．

【解析】

（1）由在△ABC中，AB=AC，∠BAC=120°，可求得∠B与∠C的度数，又由AB的垂直平分线交AB于E，交BC于M；可得AM=BM，继而求得∠MAB的度数，则可求得∠AMN的度数，同样方法得出∠ANM的度数，继而求得答案；
（2）先得△AMN为等边三角形，则可得AM=AN=MN，又由BM=AM，CN=AN，即可证得结论．

（1）解：∵AB=AC，∠A=120°，
∴∠B=∠C=30°，
∵直线ME垂直平分AB，
∴BM=AM，
∴∠B=∠MAB=30°，
∴∠AMN=∠B+∠MAB=60°，
同理可得：∠ANM=60°．
∴∠MAN=180°-60°-60°=60°；
（2）证明：∵在△AMN中，∠AMN=∠ANM=∠MAN=60°，
∴△AMN为等边三角形．
即AM=AN=MN，
又∵BM=AM，CN=AN，
∴BM=CN．