题目内容
【题目】如图，在正方形ABCD中，E为AB的中点，FE⊥AB，AF=2AE，FC交BD于O，则∠DOC的度数为（ ）
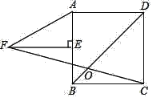
A. 75° B. 54° C. 60° D. 67.5°
【答案】C
【解析】
如图，连接DF、BF．首先证明∠FDB=
∠FAB=30°，再根据全等三角形的判定证明△FAD≌△FBC，推出∠ADF=∠FCB=15°，由此即可解决问题．
解：如图，连接DF、BF．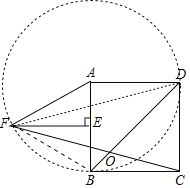
∵FE⊥AB，AE=EB，
∴FA=FB，
∵AF=2AE，
∴AF=AB=FB，
∴△AFB是等边三角形，
∵AF=AD=AB，
∴点A是△DBF的外接圆的圆心，
∴∠FDB=∠FAB=30°，
∵四边形ABCD是正方形，
∴AD=BC，∠DAB=∠ABC=90°，∠ADB=∠DBC=45°，
∴∠FAD=∠FBC，
∴△FAD≌△FBC，
∴∠ADF=∠FCB=15°，
∴∠DOC=∠OBC+∠OCB=60°．
故选：C．
练习册系列答案
相关题目
