题目内容
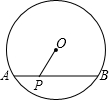
如图，⊙O的直径为10cm，弦AB为8cm，P是弦AB上一点，若OP的长为整数，则满足条件的点P有（ ）
| A．2个 | B．3个 | C．4个 | D．5个 |
如图，连接OA，过O作OD⊥AB于D，
∵⊙O的直径为10cm，弦AB为8cm，
当OP⊥AB时OP有最小值，
则AD=
AB=4cm，
由勾股定理得OD=
=
=3cm，
∴当OP⊥AB时OP的最小值为3，
当OP与OA重合时P最大为5，
∴P在AD中间有3，4，5三个整数点，
在BD之间有4，5，两个整数点，
故P在AB上有5个整数点．
故选D．
∵⊙O的直径为10cm，弦AB为8cm，
当OP⊥AB时OP有最小值，
则AD=
| 1 |
| 2 |
由勾股定理得OD=
| OA2-AD2 |
| 52-42 |
∴当OP⊥AB时OP的最小值为3，
当OP与OA重合时P最大为5，
∴P在AD中间有3，4，5三个整数点，
在BD之间有4，5，两个整数点，
故P在AB上有5个整数点．
故选D．
练习册系列答案
相关题目
