题目内容
如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长交BC的延长线于点F.
(1)求证:∠BDF=∠F;
(2)如果CF=1,sinA=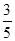 ,求⊙O的半径.
,求⊙O的半径.
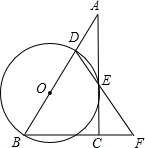
(1)求证:∠BDF=∠F;
(2)如果CF=1,sinA=
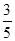 ,求⊙O的半径.
,求⊙O的半径.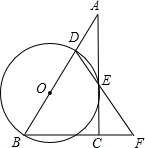
(1)证明见解析;(2)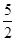 .
.
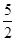 .
.试题分析:(1)连接OE,求出∠ODE=∠F=∠DEO,推出OE∥BC,得出OE⊥AC,根据切线的判定推出即可;
(2)由CF=1,sinA=
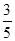 ,在Rt△ABC和Rt△AOC中分别应用锐角三角函数定义求解.
,在Rt△ABC和Rt△AOC中分别应用锐角三角函数定义求解.(1)如图,连接OE,#%源:中国教育^&出版网@]
∵AC与圆O相切,
∴OE⊥AC.
∵BC⊥AC,
∴OE∥BC.
∴∠1=∠F.
又∵OE=OD,
∴∠1=∠2.
∴∠BDF=∠F.
(2)∵sinA=
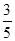 ,∴可设BC=3x, AB=5x.
,∴可设BC=3x, AB=5x.又∵CF=1,∴BF=3x+1.
由(1)得:∠BDF=∠F ,∴BD=BF.
∴BD=3x+1.中国
∴OE=OB=
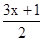 , AO=AB﹣OB=
, AO=AB﹣OB=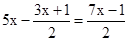 .]
.]∵ sinA=
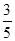 ,
,∴
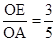 ,即
,即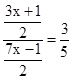 ,解得:x=
,解得:x=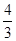 .
.∴⊙O的半径为
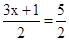 .
.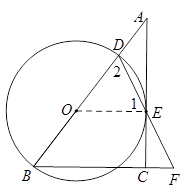

练习册系列答案
相关题目
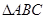 中,AB=AC,以AB为直径的
中,AB=AC,以AB为直径的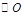 交BC于点M,
交BC于点M,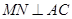 于点N.
于点N.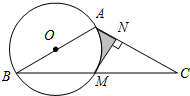
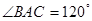 ,AB=2,求图中阴影部分的面积.
,AB=2,求图中阴影部分的面积.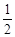 BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.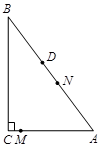
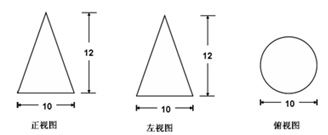
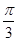 ,那么此扇形的圆心角的大小为
,那么此扇形的圆心角的大小为