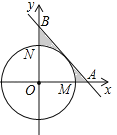题目内容
【题目】如图所示,在平面直角坐标系中A(0,2),点B(﹣3,0).△AOB绕点O逆时针旋转30°得到△A1OB1.
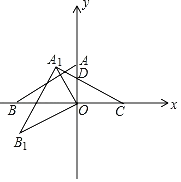
(1)直接写出点B1的坐标;
(2)点C(2,0),连接CA1交OA于点D,求点D的坐标.
【答案】(1)(﹣![]() ,﹣
,﹣![]() );(2)(0,
);(2)(0,![]() )
)
【解析】
(1)过点B1作B1E⊥y轴于点E,根据△AOB绕点O逆时针旋转30°得到△A1OB1,即可求出点B1坐标;
(2)根据题意可得OA1=OC=2,由旋转可得∠AOA1=30°,进而得∠A1OC=120°,所以可得∠A1CO=30°.从而可求出OD的长,即可得点D的坐标.
解:(1)如图,过点B1作B1E⊥y轴于点E,
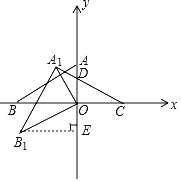
∵△AOB绕点O逆时针旋转30°得到△A1OB1,
∴∠BOB1=30°,
∴∠B1OE=60°,
∵B(﹣3,0),
∴OB=OB1=3,
∴OE=![]() ,B1E=
,B1E=![]() ,
,
∴点B1的坐标为:(﹣![]() ,﹣
,﹣![]() );
);
(2)∵点C(2,0),
∴OC=2,
∵A(0,2),
∴OA=OA1=2,
∴OA1=OC=2,
∵∠AOA1=30°,∠DOC=90°,
∴∠A1OC=120°,
∴∠A1CO=30°.
∴OD=OCtan30°=2×![]() .
.
∴点D的坐标为:(0,![]() ).
).

 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】甲、乙两店销售同一种蔬菜种子.在甲店,不论一次购买数量是多少,价格均为4.5元![]() .在乙店价格为5元
.在乙店价格为5元![]() ,如果一次购买2kg以上的种子,超出2kg部分的种子价格打8折.设小明在同一个店一次购买种子的数量为
,如果一次购买2kg以上的种子,超出2kg部分的种子价格打8折.设小明在同一个店一次购买种子的数量为![]() (
(![]() ).
).
(1)根据题意填表:
一次购买数量∕ | 1.5 | 2 | 3.5 | 6 | … |
在甲店花费∕元 | 6.75 | 15.75 | … | ||
在乙店花费∕元 | 7.5 | 16 | … |
(2)设在甲店花费![]() 元,在乙店花费
元,在乙店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
① 若小明在甲店和在乙店一次购买种子的数量相同,且花费相同,则他在同一个店一次购买种子的数量为 ![]() ;
;
② 若小明在同一个店一次购买种子的数量为3kg,则他在甲、乙两个店中的 店购买花费;
③ 若小明在同一个店一次购买种子花费了45元,则他在甲、乙两个店中的 店购买数量多.