题目内容
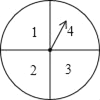
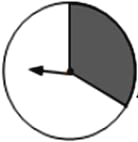
【题目】如图,转盘的白色扇形和黑色扇形的圆心角分别为240°和120°.让转盘自由转动2次,则指针一次落在白色区域,另一次落在黑色区域的概率是________.
【答案】![]()
【解析】
由白色区域是240度,黑色区域是120度,指针落在它们的可能性不相同;所以将白色区域分成相等的两部分,那么指针落在三个部分的可能性相同,则可由列表法或树状图列出所有可能的结果,利用概率公式即可求解.
解:将白色扇形分成相等的两部分,分别记为白1和白2, 所以转盘自由转动1次,指针落在白1,白2,黑三部分的可能性相同,
如下表,
白1 | 白2 | 黑 | |
白1 | (白1,白1) | (白2,白1) | (黑,白1) |
白2 | (白1,白2) | (白2,白2) | (黑,白2) |
黑 | (白1,黑) | (白2,黑) | (黑,黑) |
所有等可能的结果有9种,其中一次落在白色区域,一次落在黑色区域的有4种,所以P(指针一次落在白色区域,另一次落在黑色区域)= ![]() .
.
故答案为: ![]() .
.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A. 一副去掉大小王的普迺扑克牌洗匀后,从中任抽一张牌的花色是红桃
B. 从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
C. 抛一枚硬币,出现正面的概率
D. 抛一个质地均匀的正六面体骰子(六个面上分别标有1,2,3,4,5,6),向上的面点数是5