Question

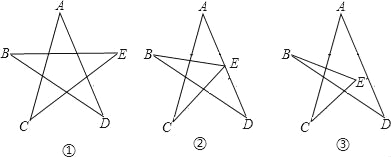
【题目】如图①所示，为五角星图案，图②、图③叫做蜕变的五角星．试回答以下问

（1）在图①中，试证明∠A+∠B+∠C+∠D+∠E=180°；

（2）对于图②或图③，还能得到同样的结论吗？若能，请在图②或图③中任选其一证明你的发现；若不能，试说明理由．

Answer 1

【答案】（1）∠A+∠B+∠C+∠D+∠E=180°．（2）结论仍然成立.

【解析】

（1）设CE与BD、AD的交点分别为M、N，可分别在△MBE和△NAC中，由三角形的外角性质求得∠DMN=∠B+∠E、∠DNM=∠A+∠C，进而在△DMN中根据三角形内角和定理得出所求的结论．
（2）图②、③的证法与图①的解法是一致的，以图③为例；
延长CE交AD于F，设CE与BD的交点为M，分别在△MBE、∠FCA中，由三角形的外角性质求得∠DMF=∠B+∠E、∠DFM=∠A+∠C，继而在△DMF中，根据三角形内角和定理得到所求的结论．

解：∠A+∠B+∠C+∠D+∠E=180°．

（1）证明：如图①，设BD、AD与CE的交点为M、N；

△MBE和△NAC中，由三角形的外角性质知：

∠DMN=∠B+∠E，∠DNM=∠A+∠C；

△DMN中，∠DMN+∠DNM+∠D=180°，

故∠A+∠B+∠C+∠D+∠E=180°．

（2）结论仍然成立，以图③为例；

延长CE交AD于F，设CE与BD的交点为M；

同（1）可知：∠DMF=∠B+∠E，∠DFM=∠A+∠C；

在△DMF中，∠D+∠DMF+∠DFM=180°，

∴∠A+∠B+∠C+∠D+∠E=180°．