题目内容
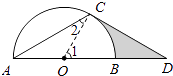
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
【答案】
(1)
证明:连接OC.
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.即OC⊥CD,
∴CD是⊙O的切线.
(2)
解:∵∠A=30°,
∴∠1=2∠A=60°.
∴S扇形BOC= ![]() .
.
在Rt△OCD中,
∵ ![]() ,
,
∴CD=2 ![]() .
.
∴ ![]() .
.
∴图中阴影部分的面积为: ![]() .
.
【解析】此题综合考查了等腰三角形的性质、切线的判定方法、扇形的面积计算方法.(1)连接OC.只需证明∠OCD=90°.根据等腰三角形的性质即可证明;(2)阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积.

练习册系列答案
相关题目
【题目】某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
学生人数(人) | 1 | 3 | 2 | 2 | 2 |
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm
B.165cm,170cm
C.170cm,165cm
D.170cm,170cm