题目内容
【题目】已知![]() 中弦
中弦![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )

A. AB=CD B. 弧AC=弧BD
C. PA=PD D. 弧AC=弧BC
【答案】D
【解析】
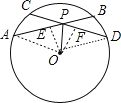
作OE⊥AB于E,OF⊥CD于F,如图,连结OA、OD,根据垂径定理得AE=BE,CF=DF,再根据角平分线定理得OE=OF,于是利用“HL”可证明Rt△AOE≌Rt△DOF,Rt△POE≌Rt△POF,得到AE=DF,PE=PF,易得AB=CD,PA=PD,则可对A选项和C选项进行判断;根据圆心角、弧、弦的关系有AB=CD得![]() ,易得
,易得![]() ,则可对B选项和D选项进行判断.
,则可对B选项和D选项进行判断.
作OE⊥AB于E,OF⊥CD于F,如图,连结OA、OD,
∵OE⊥AB,OF⊥CD,
∴AE=BE,CF=DF,
∵PO平分∠APD,
∴OE=OF,
在Rt△AOE和Rt△DOF中,
![]() ,
,
∴Rt△AOE≌Rt△DOF,
∴AE=DF,
∴AB=CD,所以A选项的结论正确;
∴![]() ,
,
∴![]() ,即
,即![]() ,所以B选项的结论正确,D选项的结论错误;
,所以B选项的结论正确,D选项的结论错误;
在Rt△POE和Rt△POF中,
![]() ,
,
∴Rt△POE≌Rt△POF,
∴PE=PF,
∴AE+PE=DF+PF,
即PA=PD,所以C选项的结论错误.
故选D.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目