题目内容
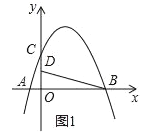
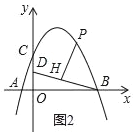
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于点A(﹣2,0)和B(B在A右侧),交y轴于点C,直线y=![]() 经过点B,交y轴于点D,且D为OC中点.
经过点B,交y轴于点D,且D为OC中点.
(1)求抛物线的解析式;
(2)若P是第一象限抛物线上的一点,过P点作PH⊥BD于H,设P点的横坐标是t,线段PH的长度是d,求d与t的函数关系式;
(3)在(2)的条件下,当d=![]() 时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)P(
x+4;(2)P(![]() ,
,![]() );(3)Q(0,4).
);(3)Q(0,4).
【解析】试题分析:(1)首先求出点B坐标,利用待定系数法即可解决问题.
(2)设P(t,﹣![]() t2+
t2+![]() t+4),,由cos∠HPM=cos∠DBO,可得
t+4),,由cos∠HPM=cos∠DBO,可得![]() ,由此构建二次函数,利用二次函数的性质解决问题.
,由此构建二次函数,利用二次函数的性质解决问题.
(3) 过点P作PF⊥x轴于点F,过点H作HG⊥PF于点G,BD与PQ交于点N,过N作NE⊥HG于E.由全等三角形△PHG≌△HNE,的性质,(2)中函数解析式求得点P、N的坐标,然后由直线与抛物线的解析式求得交点Q的坐标.
解:(1)∵y=2kx﹣12k 经过B点,
∴当y=0,x=6,
∴B(6,0),又∵A(﹣2,0),
∴![]() ,
,
解得![]() ,
,
∴y=﹣![]() x2+
x2+![]() x+4.
x+4.
(2)如图,过点P作PM∥y轴交BD于点M,设P(t,﹣![]() t2+
t2+![]() t+4),
t+4),
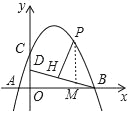
∵CD=OD,
当x=0时y=4,
∴C(0,4)
∴OD=2,
∴D(0,2),
∴BD=2![]() ,
,
设直线BD解析式为y=mx+n,
∴6m+n=0,n=2,
∴yBD=﹣![]() x+2,
x+2,
∴M(t,﹣![]() t+2),
t+2),
∴PM=﹣![]() t2+
t2+![]() t+2,
t+2,
∵∠HPM=∠DBO,
∴cos∠HPM=cos∠DBO,
∴![]() =
=![]() ,
,
∴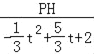 =
=![]() ,
,
∴d=﹣![]() t2+
t2+![]() t+
t+![]() ,
,
∴d=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,PH值最大,
时,PH值最大,
∴P(![]() ,
,![]() ).
).
(3)过点P作PF⊥x轴于点F,过点H作HG⊥PF于点G,BD与PQ交于点N,过N作NE⊥HG于E.
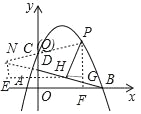
∵∠HPN=45°,PH⊥BD,
∴PH=HN,
∴△PHG≌△HNE,
∴HG=NE,PG=EH,
∵由(2)知,d=﹣![]() t2+
t2+![]() t+
t+![]() ,即:d=﹣
,即:d=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,PH=
时,PH=![]() ,
,
∴P(![]() ,
,![]() ).
).
当PH=![]() 时,HG=
时,HG=![]() PG=
PG=![]() ,
,
∴EH=![]() ,EN=
,EN=![]() ,
,
∴N(﹣![]() ,
,![]() ),P(
),P(![]() ,
,![]() ),
),
∴yPN=![]() x+4,
x+4,
由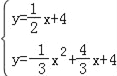 ,
,
解得![]() 或
或![]() ,
,
∴Q(0,4).

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案