��Ŀ����
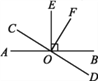
����Ŀ���������������֪��AOB��70�㣬��AOD��![]() ��AOC����BOD��3��BOC����BOC��45�㣩�����BOC�Ķ�����
��AOC����BOD��3��BOC����BOC��45�㣩�����BOC�Ķ�����
������˼����������С���÷������۵ķ��������
��1��������OC�ڡ�AOB���ڲ�ʱ����������OD�ڡ�AOC�ڲ�����ͼ1�������BOC�Ķ��������������£�
���BOC���������BOD��3��BOC��3�������COD����BOD����BOC��2�������AOD��![]() ��AOC��
��AOC��
���AOD����COD��2�������AOB����AOD+��BOD��2��+3����5����70�㣬�����14�㣬���BOC��14��
�ʣ�������OC�ڡ�AOB���ڲ�ʱ����������OD�ڡ�AOB�ⲿ����ͼ2�����������BOC�Ķ�����
���������졿��2��������OC�ڡ�AOB���ⲿʱ�����㻭��ͼ�Σ������BOC�Ķ�����
����������������������BOC�Ķ����ֱ����� ����
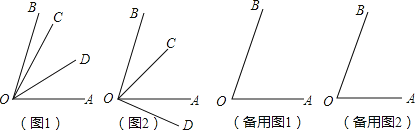
���𰸡���1���ڡ�BOC=30������2����ͼ����������BOC�Ķ����ֱ���14����30����10����42����
���������������: ��1��������֪�����ó���COD����AOD����AOB���BOC�Ĺ�ϵ�������BOC�Ķ�����
��2���������ۣ����ݡ�AOD����BOD����AOB���BOC�Ĺ�ϵ���ó���BOC�Ķ�����
�������:
��1�������BOC=�������BOD=3����������OD�ڡ�AOB�ⲿ����ͼ2��
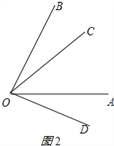
��COD=��BOD����BOC=2����
�ߡ�AOD=![]() ��AOC��
��AOC��
���AOD=![]() ��COD=
��COD= ![]() ��
��
���AOB=��BOD����AOD=3����![]() =
= ![]() =70����
=70����
����=30�������BOC=30����
��2��������OC�ڡ�AOB�ⲿʱ���������⣬��ʱ����OC��������OB��
�ߡ�BOC��45������AOD=![]() ��AOC��
��AOC��
������OD��λ��Ҳֻ�����ֿ��ܣ�
��������OD�ڡ�AOB�ڲ�����ͼ3��ʾ��
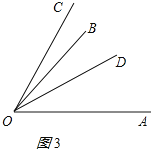
���COD=��BOC+��COD=4����
���AOB=��BOD+��AOD=3��+4��=7��=70����
����=10����
���BOC=10����
��������OD�ڡ�AOB�ⲿ����ͼ4��
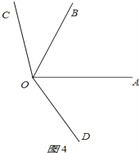
���COD=��BOC+��BOD=4����
�ߡ�AOD=![]() ��AOC��
��AOC��
���AOD=![]() ��COD=
��COD=![]() ����
����
���AOB=��BOD����AOD=3����![]() ��=
��=![]() ��=70����
��=70����
����=42����
���BOC=42����
������������BOC�Ķ����ֱ���14����30����10����42����

 ��У����ϵ�д�
��У����ϵ�д�