Question

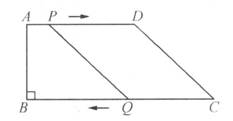
如图，四边形ABCD是直角梯形，∠B＝90°，AB＝8cm，AD＝24cm，BC＝26cm．点P从A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向B运动．其中一个动点到达端点时，另一个动点也随之停止运动．从运动开始，经过多少时间，四边形PQCD成为平行四边形？成为等腰梯形？

Answer 1

答案：略
解析：

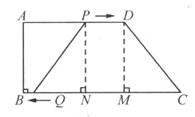
如图(1)所示，设经过ts，四边形PQCD成为平行四边形．此时PD＝CQ．所以24－t＝3t所以t＝6．所以经过6s，四边形PQCD成为平行四边形． 如图(2)所示，设经过ts，四边形PQCD成为等腰梯形．分别过D、P作DM⊥BC于M，PN⊥BC于N，易得四边形ABMD和PNMD都是矩形．此时QN＝MC＝BC－BM＝BC－AD＝26－24＝2(cm)．QN＝BN－BQ＝AP－BQ＝t－(26－3t)＝4t－26(cm)．所以4t－26＝2．所以t＝7．所以经过7s，四边形PQCD成为等腰梯形．                        (1)                                                    (2)