题目内容
【题目】设△ABC的面积为1.
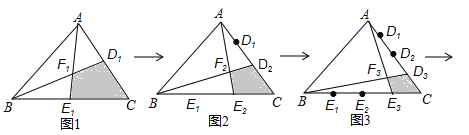
如图1,分别将AC,BC边2等分,D1,E1是其分点,连接AE1,BD1交于点F1,得到四边形CD1F1E1,其面积S1=![]() .
.
如图2,分别将AC,BC边3等分,D1,D2,E1,E2是其分点,连接AE2,BD2交于点F2,得到四边形CD2F2E2,其面积S2=![]() ;
;
如图3,分别将AC,BC边4等分,D1,D2,D3,E1,E2,E3是其分点,连接AE3,BD3交于点F3,得到四边形CD3F3E3,其面积S3=![]() ;
;
…
按照这个规律进行下去,若分别将AC,BC边(n+1)等分,…,得到四边形CDnEnFn,其面积S= .
【答案】![]() .
.
【解析】
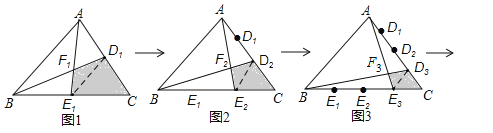
试题分析:如图所示,连接D1E1,D2E2,D3E3,∵图1中,D1,E1是△ABC两边的中点,∴D1E1∥AB,D1E1=![]() AB,∴△CD1E1∽△CBA,且
AB,∴△CD1E1∽△CBA,且![]() =
=![]() ,∴S△CD1E1=
,∴S△CD1E1=![]() S△ABC=
S△ABC=![]() ,∵E1是BC的中点,∴S△BD1E1=S△CD1E1=
,∵E1是BC的中点,∴S△BD1E1=S△CD1E1=![]() ,∴S△D1E1F1=
,∴S△D1E1F1=![]() S△BD1E1=
S△BD1E1=![]() ×
×![]() =
=![]() ,∴S1=S△CD1E1+S△D1E1F1=
,∴S1=S△CD1E1+S△D1E1F1=![]() +
+![]() =
=![]() ,同理可得:
,同理可得:
图2中,S2=S△CD2E2+S△D2E2F2=![]() =
=![]() ,图3中,S3=S△CD3E3+S△D3E3F3=
,图3中,S3=S△CD3E3+S△D3E3F3=![]() =
=![]() ,以此类推,将AC,BC边(n+1)等分,得到四边形CDnEnFn,其面积Sn=
,以此类推,将AC,BC边(n+1)等分,得到四边形CDnEnFn,其面积Sn=![]() =
=![]() ,故答案为:
,故答案为:![]() .
.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目