题目内容
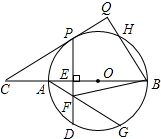 已知:如图,AB为⊙O的直径,C是BA延长线上一点,CP切⊙O于P,弦PD⊥AB于E,过点B作BQ⊥CP于Q,交⊙O于H,G是
已知:如图,AB为⊙O的直径,C是BA延长线上一点,CP切⊙O于P,弦PD⊥AB于E,过点B作BQ⊥CP于Q,交⊙O于H,G是 |
| AB |
 |
| BG |
| 1 |
| 3 |
 |
| AB |
| 3 |
| 3 |
求:(1)∠C的度数;
(2)△AEF和△ABG的面积;
(3)QH的长.
分析:(1)连接OP,求出∠OPC=90°,∠BAF=30°,设EF=x,则AE=
,BE=3
x,AB=4
x,OB=2
x,OE=
x,根据cos∠POA=
=
,求出∠POA=60°即可;
(2)由垂径定理得出PE=
PD=3
,在△CPE中,由勾股定理求出x=
,求出AE=
x=3,EF=
,根据三角形的面积公式求出即可;根据AB=4
x=12,求出∠BAG=30°,推出BG=6,由勾股定理求出AG=6
,根据三角形的面积公式求出即可;
(3)由勾股定理求出CP=6
,由切割线定理得出PC2=AC×BC,求出AC=6,BC=18,根据∠C=30°,∠Q=90°求出BQ=
BC=9,由勾股定理求出CQ=9
,PQ=3
,由切割线定理得出PQ2=QH×BQ,代入求出即可.
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| OE |
| OP |
| 1 |
| 2 |
(2)由垂径定理得出PE=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
(3)由勾股定理求出CP=6
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
解答:(1)解:连接OP,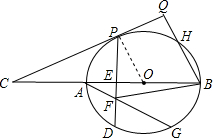
∵CP切⊙O于P,
∴∠OPC=90°,
∵
=
,
∴∠BAF=30°,
设EF=x,则AE=
x,
∵tan∠BFE=3
,
∴BE=3
x,
AB=4
x,OB=2
x,OE=
x,
∴cos∠POA=
=
,
∴∠POA=60°,
∴∠C=90°-60°=30°;
(2)解:由垂径定理得:PE=
PD=3
,
∵在△OPE中,由勾股定理得:OP2=OE2+PE2,
∴(2
x)2=(
x)2+(3
)2,
x=
,
∴AE=
x=3,EF=
,
∴S△AEF=
×AE×EF=
×3×
=
,
∵AB=4
x=12,
∴∠BAG=30°,
∴BG=6,
由勾股定理的:AG=6
,
∴S△ABG=
×AG×BG=
×6
×6=18
;
(3)解:∵由(2)知:OE=
x=3,OP=2
x=6,AB=12,∠C=30°,
∴OC=12,
由勾股定理得:CP=6
,
∵CP是切线,CAB是割线,由切割线定理得:PC2=AC×BC,
∴(6
)2=AC×(AC+12),
AC=6,
∴BC=18,
∵∠C=30°,∠Q=90°,
∴BQ=
BC=9,
∴由勾股定理得:CQ=9
,
∴PQ=3
,
∵由切割线定理得:PQ2=QH×BQ,
(3
)2=9QH,
∴QH=3.
答:QH的长是3.

∵CP切⊙O于P,
∴∠OPC=90°,
∵
 |
| BG |
| 1 |
| 3 |
 |
| AB |
∴∠BAF=30°,
设EF=x,则AE=
| 3 |
∵tan∠BFE=3
| 3 |
∴BE=3
| 3 |
AB=4
| 3 |
| 3 |
| 3 |
∴cos∠POA=
| OE |
| OP |
| 1 |
| 2 |
∴∠POA=60°,
∴∠C=90°-60°=30°;
(2)解:由垂径定理得:PE=
| 1 |
| 2 |
| 3 |
∵在△OPE中,由勾股定理得:OP2=OE2+PE2,
∴(2
| 3 |
| 3 |
| 3 |
x=
| 3 |
∴AE=
| 3 |
| 3 |
∴S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
∵AB=4
| 3 |
∴∠BAG=30°,
∴BG=6,
由勾股定理的:AG=6
| 3 |
∴S△ABG=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(3)解:∵由(2)知:OE=
| 3 |
| 3 |
∴OC=12,
由勾股定理得:CP=6
| 3 |
∵CP是切线,CAB是割线,由切割线定理得:PC2=AC×BC,
∴(6
| 3 |
AC=6,
∴BC=18,
∵∠C=30°,∠Q=90°,
∴BQ=
| 1 |
| 2 |
∴由勾股定理得:CQ=9
| 3 |
∴PQ=3
| 3 |
∵由切割线定理得:PQ2=QH×BQ,
(3
| 3 |
∴QH=3.
答:QH的长是3.
点评:本题考查了切线的性质,切割线定理,勾股定理,三角形的面积,含30度角的直角三角形等知识点的应用,主要考查学生运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA=
(2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA= 已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.
已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°. 已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为
已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为 已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①
已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①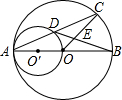 已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.
已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.