��Ŀ����
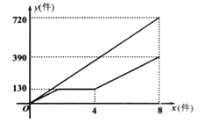
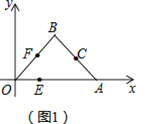
����Ŀ����֪���磨ͼ1������ƽ��ֱ�������У�A(12��0)��B(6��6)����CΪ�߶�AB���е㣬��D��ԭ��O���ڵ�C�Գƣ�
��1������ֱ�ߺ�Բ���ڣ�ͼ1����������D��λ�ã�������ͼ�ۼ������ж��ı���OBDA����״����˵�����ɣ�
��2���ڣ�ͼ1���У�����E�ӵ�O��������ÿ��1����λ���ٶ����߶�OA�˶��������Aʱֹͣ��ͬʱ������F�ӵ�O��������ÿ��a����λ���ٶ���OB��BD��DA�˶��������Aʱֹͣ�����˶���ʱ��Ϊt���룩��
�ٵ�t=4ʱ��ֱ��EFǡ��ƽ���ı���OBDA���������a��ֵ��
�ڵ�t=5ʱ��CE=CF����ֱ��д��a��ֵ��
���𰸡���1���ı���OBDA��ƽ���ı��Σ�����������2����2+![]() ����
����![]() ��
��![]() ��
��![]()
��������
��1��������OC����ȡCD=OC��Ȼ���ɶԽ�����ƽ�ֵ��ı�����ƽ���ı��ν��пɵõ��ı��ε���״��
��2������ֱ��EFǡ��ƽ���ı���OBDA�������ֱ֪��EF�ع�C����������֤����OEC�ա�DFC���Ӷ������DF�ij��ȣ����ǵõ�BF=8��Ȼ�����������ľ��빫ʽ���OB�ij����Ӷ������a��ֵ��
������õ�E�����꣬Ȼ�����EC�ij����Ӷ��õ�CF1�ij���Ȼ�����ݹ��ɶ������涨��֤����OBA=90��������BCF1�У����ݹ��ɶ��������BF1�ij����Ӷ������a��ֵ�����F2�����꣨b��6������CE=CF�г�����b�ķ��̿���õ�F2�����꣬�Ӷ������a��ֵ����Rt��CAF3�У�ȡ��AF3�ij����Ӷ���õ�F�˶���·�̣����ǿ����a��ֵ��
�⣺��1����ͼ��ʾ��
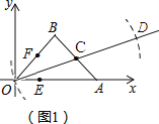
�ı���OBDA��ƽ���ı��Σ�
�������£��ߵ�CΪ�߶�AB���е㣬
��CB=CA��
�ߵ�D��ԭ��O���ڵ�C�Գƣ�
��CO=CD��
���ı���OBDA��ƽ���ı��Σ�
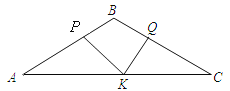
��2������ͼ2��ʾ��
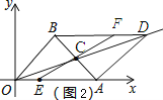
��ֱ��EFǡ��ƽ���ı���OBDA�������
��ֱ��EF�ع�C��9��3����
��t=4��
��OE=4��
��BD��OA��
���COE=��CDF��
������OEC����DFC�� ��
��
���OEC�ա�DFC��
��DF=OE=4��
��BF=12-4=8��
�������ľ��빫ʽ��֪OB=![]() =6
=6![]() ��
��
��4a=6![]() +8��
+8��
��a=2+![]() ��
��
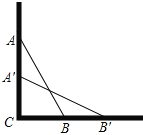
����ͼ3��ʾ��
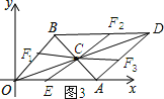
�ߵ�t=5ʱ��OE=5��
���E�����꣨5��0����
�������ľ��빫ʽ��֪EC=![]() =5��
=5��
��CE=CF��
��CF=5��
�������ľ��빫ʽ��֪OB=BA=6![]() ��
��
�֡�OA=12��
���OBAΪֱ�������Σ�
���OBA=90����
����ֱ����F1BC�У�CF1=5��BC=3![]() ��
��
��BF1=![]() ��
��
��OF1=6![]() -
-![]() ��
��
��a=![]() ��
��
����F2������Ϊ��b��6�����������ľ��빫ʽ��֪![]() =5��
=5��
��ã�b=5����ȥ����b=13��
��BF2=13-6=7��
��OB+BF2=6![]() +7��
+7��
��a=![]() ��
��
�ۡ�BO��AD��
���BAD=��OBA=90����
��AF3=![]() =
=![]() ��
��
��DF3=6![]() -
-![]() ��
��
��OB+BD+DF3=6![]() +12+6
+12+6![]() -
-![]() =12
=12![]() -
-![]() +12��
+12��
��a=![]() ��
��
��������a��ֵΪ![]() ��
��![]() ��
��![]() ��
��

 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�