题目内容
【题目】一架云梯AB长25米,如图那样斜靠在一面墙AC上,这时云梯底端B离墙底C的距离BC为7米.
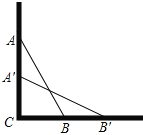
(1)这云梯的顶端距地面AC有多高?
(2)如果云梯的顶端A下滑了4米,那么它的底部B在水平方向向右滑动了多少米?
【答案】(1)24m高(2)8m.
【解析】
试题分析:(1)在直角三角形ABC中,利用勾股定理即可求出AC的长;
(2)首先求出AC的长,利用勾股定理可求出B′C的长,进而得到BB′=CB′﹣CB的值.
解:(1)在Rt△ABC中,由勾股定理得AC2+BC2=AB2,
即AC2+72=252,
所以AC=24(m),
即这架云梯的顶端A距地面有24m高;
(2)梯子的底端在水平方向也滑动了8m.
理由:∵云梯的顶端A下滑了4m至点A,
∴AC=AC﹣A′A=24﹣4=20(m),
在Rt△ACB′中,由勾股定理得AC2+BC′2=AB′2,
即202+B′C2=252
所以B′C=15(m)
BB′=CB′﹣BB=15﹣7=8(m),
即梯子的底端在水平方向也滑动了8m.

练习册系列答案
相关题目

