题目内容
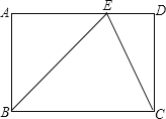
【题目】如图，在矩形ABCD中，点E在AD上，且EC平分∠BED．
（1）△BEC是否为等腰三角形？证明你的结论；
（2）若AB=2，∠DCE=22.5°，求BC长．
【答案】（1）△BEC是等腰三角形，见解析；（2）2
【解析】
（1）由矩形的性质和角平分线的定义得出∠DEC=∠ECB=∠BEC，推出BE=BC即可；
（2）证出AE=AB=2，根据勾股定理求出BE，即可得出BC的长．
解：（1）△BEC是等腰三角形；理由如下：
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠DEC=∠BCE，
∵EC平分∠DEB，
∴∠DEC=∠BEC，
∴∠BEC=∠ECB，
∴BE=BC，即△BEC是等腰三角形．
（2）∵四边形ABCD是矩形，
∴∠A=∠D=90°，
∵∠DCE=22.5°，
∴∠DEB=2×（90°-22.5°）=135°，
∴∠AEB=180°-∠DEB=45°，
∴∠ABE=∠AEB=45°，
∴AE=AB=2，
由勾股定理得：BC=BE=
=
=2
，
答：BC的长是2．
练习册系列答案
相关题目
【题目】汽车油箱中的余油量
（升）随汽车行驶的时间
（时）的变化而变化，与之间的关系为
，其中
是油箱中原有的油的升数，若这辆汽车油箱中原有油60升．
（1）用表格表示行驶1到5小时过程中这辆汽车油箱中余油量与行驶时间的关系，填写下表：
行驶时间（时） | 1 | 2 | 3 | 4 | 5 |
余油量（升） |
（2）这辆车最多可行驶多少小时？
