Question

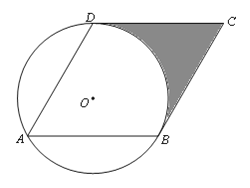
【题目】已知：如图，已知⊙O的半径为1，菱形ABCD的三个顶点A、B、D在⊙O上，且CD与⊙O相切．

（1）求证：BC与⊙O相切；

（2）求阴影部分面积．

Answer 1

【答案】（1）证明见解析；（2）－

【解析】试题分析：（1）连结OB、OD、OC，只要证明△OCD≌△OCB，推出∠ODC=∠OBC，由CD与⊙O相切推出OD⊥CD，推出∠OBC=∠ODC=90°，由此即可证明；
（2）根据S阴影=2S△DOC-S扇形OBD计算即可；

试题解析：（1）连结OB、OD、OC，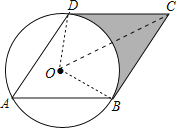

∵ABCD是菱形，
∴CD=CB，
∵OC=OC，OD=OB，
∴△OCD≌△OCB，
∴∠ODC=∠OBC，
∵CD与⊙O相切，∴OD⊥CD，
∴∠OBC=∠ODC=90°，
即OB⊥BC，点B在⊙O上，
∴BC与⊙O相切．
（2）∵ABCD是菱形，
∴∠A=∠DCB，
∵∠DOB与∠A所对的弧都是
∴∠DOB=2∠A，
由（1）知∠DOB+∠C=180°，
∴∠DOB=120°，∠DOC=60°，
∵OD=1，∴OC=2，DC=
∴S阴影=2S△DOC-S扇形OBD=2××1×-=．