题目内容
【题目】如图,AD=CB,E,F是AC上两动点,且有DE=BF. 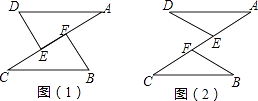
(1)若点E,F运动至如图(1)所示的位置,且有AF=CE,求证:△ADE≌△CBF;
(2)若点E,F运动至如图(2)所示的位置,仍有AF=CE,则△ADE≌△CBF还成立吗?为什么?
(3)若点E,F不重合,则AD和CB平行吗?请说明理由.
【答案】
(1)证明:∵AF=CE,
∴AF+EF=CE+EF,即AE=CF,
在△ADE和△CBF中,
∵ 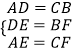 ,
,
∴△ADE≌△CBF(SSS)
(2)解:△ADE≌△CBF成立,
∵AF=CE,
∴AF﹣EF=CE﹣EF,即AE=CF,
在△ADE和△CBF中,
∵ 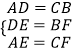 ,
,
∴△ADE≌△CBF(SSS)
(3)解:AD∥CB,
∵△ADE≌△CBF,
∴∠A=∠C,
∴AD∥CB
【解析】(1)由AF=CE知AF+EF=CE+EF,即AE=CF,又AD=CB、DE=BF可证△ADE≌△CBF;(2)由AF=CE知AF﹣EF=CE﹣EF,即AE=CF,又AD=CB、DE=BF可证△ADE≌△CBF;(3)根据(1)(2)可知△ADE≌△CBF,故∠A=∠C,可得AD∥CB.
【考点精析】利用平行线的判定对题目进行判断即可得到答案,需要熟知同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目