题目内容
【题目】如图，已知一次函数y＝kx+b的图象经过A（﹣1，﹣5），B（0，﹣4）两点且与x轴交于点C，二次函数y＝ax2+bx+4的图象经过点A、点C．
（1）求一次函数和二次函数的函数表达式；
（2）连接OA，求∠OAB的正弦值；
（3）若点D在x轴的正半轴上，是否存在以点D，C，B构成的三角形与△OAB相似？若存在，求出点D的坐标；若不存在，请说明理由．
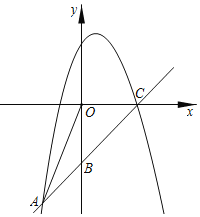
【答案】（1）y＝x﹣4，y＝﹣2x2+7x+4；（2）
；（3）存在，（6，0）或（20，0）
【解析】
（1）利用待定系数法求出一次函数的解析式，然后根据与x轴的交点y=0，求出C的坐标，然后根据A与C的坐标求出二次函数的解析式即可；
（2）过O作OH⊥BC，垂足为H，证明△BOC为等腰直角三角形，求出OH＝
BC＝2
，然后求出OA，即可求出∠OAB的正弦值；
（3）利用勾股定理求出AH，再求出AB＝，然后分情况求出D点的坐标即可.
解：（1）∵一次函数y＝kx+b的图象经过A（﹣1，﹣5），B（0，﹣4）两点，
∴﹣5＝﹣k+b，b＝﹣4，k＝1，
∴一次函数解析式为：y＝x﹣4，
∵一次函数y＝x﹣4与x轴交于点C，
∴y＝0时，x＝4，
∴C（4，0），
∵二次函数y＝ax2+bx+4的图象经过点A（﹣1，﹣5）、点C（4，0），
∴
，
解得a＝﹣2，b＝7，
∴二次函数的函数表达式为y＝﹣2x2+7x+4；
（2）过O作OH⊥BC，垂足为H，
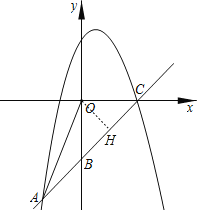
∵C（4，0），B（0，﹣4），
∴OB＝OC＝4，即△BOC为等腰直角三角形，
∴BC＝
＝
＝4，
∴OH＝BC＝2，
由点O（0，0），A（﹣1，﹣5），得：OA＝
，
在Rt△OAH中，sin∠OAB＝
＝
＝；
（3）存在，
由（2）可知，△OBC为等腰直角三角形，OH＝BH＝2，
在Rt△AOH中，根据勾股定理得：AH＝
＝
＝3，
∴AB＝AH﹣BH＝，
∴当点D在C点右侧时，∠OBA＝∠DCB＝135°，
①当
，即
时，解得CD＝2，
∵C（4，0），即OC＝4，
∴OD＝OC+CD＝2+4＝6，
此时D坐标为（6，0）；
②当
，即
时，
解得CD＝16，
∵C（4，0），即OC＝4，∴OD＝OC+CD＝16+4＝20，
此时D坐标为（20，0），
综上所述，若△BCD与△ABO相似，此时D坐标为（6，0）或（20，0）．
