Question

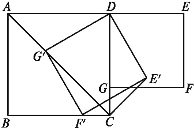
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE'F'G',此时点G'在AC上,连接CE',则CE'+CG'=______

Answer 1

【答案】

【解析】

作G′R⊥BC于R，则四边形RCIG′是正方形．首先证明点F′在线段BC上，再证明CH=HE′即可解决问题．

作G′R⊥BC于R，则四边形RCIG′是正方形．

∵∠DG′F′=∠IG′R=90°，

∴∠DG′I=∠RG′F′，

在△G′ID和△G′RF中

，

∴△G′ID≌△G′RF，

∴∠G′ID=∠G′RF′=90°，

∴点F′在线段BC上，

在Rt△E′F′H中，∵E′F′=2，∠E′F′H=30°，

∴E′H=E′F′=1，F′H=，

易证△RG′F′≌△HF′E′，

∴RF′=E′H，RG′=RC=F′H，

∴CH=RF′=E′H，

∴CE′=，

∵RG′=HF′=，

∴CG′=RG′=，

∴CE′+CG′=+．

故答案为：+．